



Next: 4.4 Summary
Up: 4.3 SR measurements
Previous: Zero- and longitudinal-field measurements
Comparing the temperature dependence of the muon T1 relaxation rate
(Fig.33) with that of 63Cu-NMR
(Fig.28), one question may arise: why the
temperature dependence is opposite between  SR and NMR. In
the NMR measurements, the T1 relaxation increased at higher
temperatures, as has been ascribed to the excitation over the spin
gap, while in
SR and NMR. In
the NMR measurements, the T1 relaxation increased at higher
temperatures, as has been ascribed to the excitation over the spin
gap, while in  SR, it decreased as shown in Fig.33.
As discussed below, the qualitatively different temperature
dependence of the T1 relaxation rates may be attributed
to the different scales of the experimental time windows.
SR, it decreased as shown in Fig.33.
As discussed below, the qualitatively different temperature
dependence of the T1 relaxation rates may be attributed
to the different scales of the experimental time windows.
The time window of the  SR method is typically
SR method is typically  , and for NMR, it is
, and for NMR, it is  . Therefore, in the paramagnetic fluctuation regime, NMR
is more capable of detecting faster fluctuations than
. Therefore, in the paramagnetic fluctuation regime, NMR
is more capable of detecting faster fluctuations than  SR. As has
been shown by gap excitation type temperature dependence
[52], the 63Cu nuclear spin relaxation
is most likely caused by magnetic excited states which produce fast
field fluctuations. From a simple scaling argument below, these
excited states do not cause fast enough muon spin relaxation
detectable in the
SR. As has
been shown by gap excitation type temperature dependence
[52], the 63Cu nuclear spin relaxation
is most likely caused by magnetic excited states which produce fast
field fluctuations. From a simple scaling argument below, these
excited states do not cause fast enough muon spin relaxation
detectable in the  SR time window.
SR time window.
The only difference between the muon spin relaxation and the 63Cu
nuclear spin relaxation is the gyromagnetic ratio of the probe spins
( and
and  ) and the electron-nuclear spin
coupling strength, which reflects the probe spin site. From previous
Knight-shift and susceptibility measurements, the hyperfine
coupling parameter between a 63Cu nuclear spin and electron
moments has been obtained as [52]:
) and the electron-nuclear spin
coupling strength, which reflects the probe spin site. From previous
Knight-shift and susceptibility measurements, the hyperfine
coupling parameter between a 63Cu nuclear spin and electron
moments has been obtained as [52]:
where the suffix (c and ab) indicates the crystalline orientation
of the parameter.
The coupling between a muon spin and the electron moments is probably
a dipolar coupling, and its magnitude can be estimated from the static
field-width of the ordered 3-leg ladder system
(Fig.29):
The gyromagnetic ratio of the two probe spins are [28,61]:
Using these parameters and the T1 relaxation formula [34],
the scaling factor of the muon/63Cu T1 relaxation rates
is estimated as:
Since the 63Cu T1 relaxation rate in the 2-leg ladder system
is  [sec-1]
(Fig.28), the corresponding muon spin
relaxation rate should be
[sec-1]
(Fig.28), the corresponding muon spin
relaxation rate should be  [
[ ] at
room temperature, and smaller at lower temperatures (see the
right axis of Fig.28). These relaxation
rates are too small for the
] at
room temperature, and smaller at lower temperatures (see the
right axis of Fig.28). These relaxation
rates are too small for the  SR time window, and therefore, the
magnetic excited states do not contribute to the muon spin relaxation.
SR time window, and therefore, the
magnetic excited states do not contribute to the muon spin relaxation.
Figure 34:
Possible muon spin relaxation mechanism. The unpaired spins
associated with the defects may cause muon spin relaxation.
 |
Then, what would be a relevant relaxation mechanism for the muon
spins? One possible scenario is that the muons detect the
unpaired spins which are related to vacancies and defects in the
system (Fig.34). From susceptibility
measurements, the amount of native unpaired moments has been
estimated as 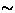 0.26 at.% of the copper ions [51].
The idea of the relaxation from the unpaired moments qualitatively
explains the general temperature and longitudinal field dependence of
the muon relaxation rate; since the couplings between the unpaired
spins are presumably small, these spins should remain paramagnetic
down to the milli-Kelvin regime, giving a temperature-independent
relaxation rate (
0.26 at.% of the copper ions [51].
The idea of the relaxation from the unpaired moments qualitatively
explains the general temperature and longitudinal field dependence of
the muon relaxation rate; since the couplings between the unpaired
spins are presumably small, these spins should remain paramagnetic
down to the milli-Kelvin regime, giving a temperature-independent
relaxation rate ( K in Fig.33).
At higher temperatures, the unpaired spins may have additional
fluctuations related to the magnetic excited states; in this
situation, the muon spin relaxation rate should decrease, and respond
less to the longitudinal fields (see data at
K in Fig.33).
At higher temperatures, the unpaired spins may have additional
fluctuations related to the magnetic excited states; in this
situation, the muon spin relaxation rate should decrease, and respond
less to the longitudinal fields (see data at  K in
Fig.33), reflecting more dynamic local
fields.
K in
Fig.33), reflecting more dynamic local
fields.
As shown in the inset of Fig.33, we analyzed
the LF dependence of muon spin relaxation rate  with the T1 relaxation formula in dilute spin systems
(eq.33). The resulting Lorentzian field width (a) and
the field fluctuation rate (
with the T1 relaxation formula in dilute spin systems
(eq.33). The resulting Lorentzian field width (a) and
the field fluctuation rate (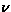 ) are shown in Table
4. In the same table, estimates of these parameters
are given, which are based on the unpaired spin concentration
from the susceptibility measurements (see the caption of Table
4 for detail.) Although the quantitative agreement
between the estimates and the experimental results is
poor, it is worth while to point out that the unpaired spins assumed here
will induce a muon spin relaxation rate (
) are shown in Table
4. In the same table, estimates of these parameters
are given, which are based on the unpaired spin concentration
from the susceptibility measurements (see the caption of Table
4 for detail.) Although the quantitative agreement
between the estimates and the experimental results is
poor, it is worth while to point out that the unpaired spins assumed here
will induce a muon spin relaxation rate ( ) which is in the time range of
) which is in the time range of
 SR measurements. Therefore, the scenario of muon spin relaxation from
the unpaired spins is better than that from the excited states. See the
concluding remark at Chapter 7 for more discussions.
SR measurements. Therefore, the scenario of muon spin relaxation from
the unpaired spins is better than that from the excited states. See the
concluding remark at Chapter 7 for more discussions.
Table 4:
The parameters in the T1 relaxation fit (2-leg ladder, 20 mK)
| Parameter |
Experiment |
Estimate |
| |
|
(native spins) |
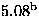 |
3.1(1) |
 |
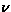 (MHz) (MHz) |
51(6) |
 |
a An estimate using eq.26. For the calculation,
the hypothetical Gaussian width ( ) with all the
spin-cites filled with static moments was taken as the Gaussian
width observed in the ordered 3-leg ladder system
(
) with all the
spin-cites filled with static moments was taken as the Gaussian
width observed in the ordered 3-leg ladder system
(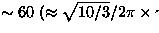 ; see
Fig.29b). The unpaired spin
concentration (
; see
Fig.29b). The unpaired spin
concentration ( ) has been estimated from the susceptibility
measurements [51]. b The dipolar fluctuation rate of
the unpaired spins, which is
) has been estimated from the susceptibility
measurements [51]. b The dipolar fluctuation rate of
the unpaired spins, which is  times larger than the Lorentzian
width (a). See the discussion in Chapter 5 for more
details of the estimation procedure.
times larger than the Lorentzian
width (a). See the discussion in Chapter 5 for more
details of the estimation procedure.




Next: 4.4 Summary
Up: 4.3 SR measurements
Previous: Zero- and longitudinal-field measurements
![]() SR method is typically
SR method is typically ![]() , and for NMR, it is
, and for NMR, it is ![]() . Therefore, in the paramagnetic fluctuation regime, NMR
is more capable of detecting faster fluctuations than
. Therefore, in the paramagnetic fluctuation regime, NMR
is more capable of detecting faster fluctuations than ![]() SR. As has
been shown by gap excitation type temperature dependence
[52], the 63Cu nuclear spin relaxation
is most likely caused by magnetic excited states which produce fast
field fluctuations. From a simple scaling argument below, these
excited states do not cause fast enough muon spin relaxation
detectable in the
SR. As has
been shown by gap excitation type temperature dependence
[52], the 63Cu nuclear spin relaxation
is most likely caused by magnetic excited states which produce fast
field fluctuations. From a simple scaling argument below, these
excited states do not cause fast enough muon spin relaxation
detectable in the ![]() SR time window.
SR time window.
![]() and
and ![]() ) and the electron-nuclear spin
coupling strength, which reflects the probe spin site. From previous
Knight-shift and susceptibility measurements, the hyperfine
coupling parameter between a 63Cu nuclear spin and electron
moments has been obtained as [52]:
) and the electron-nuclear spin
coupling strength, which reflects the probe spin site. From previous
Knight-shift and susceptibility measurements, the hyperfine
coupling parameter between a 63Cu nuclear spin and electron
moments has been obtained as [52]:
 [
[
![]() with the T1 relaxation formula in dilute spin systems
(eq.33). The resulting Lorentzian field width (a) and
the field fluctuation rate (
with the T1 relaxation formula in dilute spin systems
(eq.33). The resulting Lorentzian field width (a) and
the field fluctuation rate (![]() ) are shown in Table
4. In the same table, estimates of these parameters
are given, which are based on the unpaired spin concentration
from the susceptibility measurements (see the caption of Table
4 for detail.) Although the quantitative agreement
between the estimates and the experimental results is
poor, it is worth while to point out that the unpaired spins assumed here
will induce a muon spin relaxation rate (
) are shown in Table
4. In the same table, estimates of these parameters
are given, which are based on the unpaired spin concentration
from the susceptibility measurements (see the caption of Table
4 for detail.) Although the quantitative agreement
between the estimates and the experimental results is
poor, it is worth while to point out that the unpaired spins assumed here
will induce a muon spin relaxation rate (![]() ) which is in the time range of
) which is in the time range of
![]() SR measurements. Therefore, the scenario of muon spin relaxation from
the unpaired spins is better than that from the excited states. See the
concluding remark at Chapter 7 for more discussions.
SR measurements. Therefore, the scenario of muon spin relaxation from
the unpaired spins is better than that from the excited states. See the
concluding remark at Chapter 7 for more discussions.
![]()
![]()
![]() (MHz)
(MHz)![]()
![]() ) with all the
spin-cites filled with static moments was taken as the Gaussian
width observed in the ordered 3-leg ladder system
(
) with all the
spin-cites filled with static moments was taken as the Gaussian
width observed in the ordered 3-leg ladder system
(![]() ; see
Fig.29b). The unpaired spin
concentration (
; see
Fig.29b). The unpaired spin
concentration (![]() ) has been estimated from the susceptibility
measurements [51]. b The dipolar fluctuation rate of
the unpaired spins, which is
) has been estimated from the susceptibility
measurements [51]. b The dipolar fluctuation rate of
the unpaired spins, which is ![]() times larger than the Lorentzian
width (a). See the discussion in Chapter 5 for more
details of the estimation procedure.
times larger than the Lorentzian
width (a). See the discussion in Chapter 5 for more
details of the estimation procedure.