



Next: Longitudinal-field measurements
Up: 4.3 SR measurements
Previous: 4.3.1 The 3-leg ladder
Fig.29a shows typical zero-field
 SR spectra in the 3-leg ladder system. Below
SR spectra in the 3-leg ladder system. Below 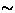 55 K, there
observed muon spin relaxation, which suggests a magnetic order of the Cu
moments. The signal amplitude was large enough to conclude that it
comes from the ladder structure, rather than from the CuO impurity
phase. The spectra below 45 K converge to 1/3 of the total
amplitude; this `1/3-component' is a signature of static order
in polycrystalline specimens (see section 3.1).
The spectra below 30 K exhibited a `dip' between
the initial decay and the 1/3-component; the existence of such a dip is
another signature of a static order. The solid line for the 50 mK data
is a phenomenological fit with the Gaussian Kubo-Toyabe function, which is
appropriate to randomly oriented, frozen dense spin systems (see
section 3.1).
55 K, there
observed muon spin relaxation, which suggests a magnetic order of the Cu
moments. The signal amplitude was large enough to conclude that it
comes from the ladder structure, rather than from the CuO impurity
phase. The spectra below 45 K converge to 1/3 of the total
amplitude; this `1/3-component' is a signature of static order
in polycrystalline specimens (see section 3.1).
The spectra below 30 K exhibited a `dip' between
the initial decay and the 1/3-component; the existence of such a dip is
another signature of a static order. The solid line for the 50 mK data
is a phenomenological fit with the Gaussian Kubo-Toyabe function, which is
appropriate to randomly oriented, frozen dense spin systems (see
section 3.1).
Figure 29:
a: Zero-field  SR spectra in the 3-leg ladder system. The solid
lines are the fit with the model function, eq.(37).
b: Temperature dependence of the Gaussian field-distribution width
(
SR spectra in the 3-leg ladder system. The solid
lines are the fit with the model function, eq.(37).
b: Temperature dependence of the Gaussian field-distribution width
(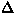 ) and the paramagnetic volume fraction (
) and the paramagnetic volume fraction (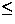 ). The
broken line is a guide to the eye.
). The
broken line is a guide to the eye.
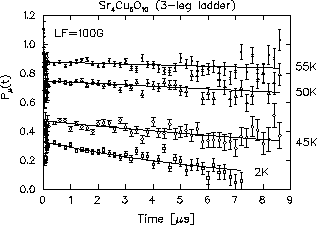 |
The spectra near the transition temperature
(Fig.29a) behave as if there is a
distribution of ordering temperatures: (1) the relaxation amplitude
(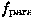 ordered volume fraction) decreases as temperature increases
and (2) the `dip' in the spectra disappears above
ordered volume fraction) decreases as temperature increases
and (2) the `dip' in the spectra disappears above  40 K, although
the relaxation is static as shown by the decay to the 1/3-component.
The absence of the dip in the static relaxation suggests a
distribution of the field-widths (
40 K, although
the relaxation is static as shown by the decay to the 1/3-component.
The absence of the dip in the static relaxation suggests a
distribution of the field-widths (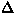 ), which would result from a distribution
in the ordering temperatures. We analyzed the
), which would result from a distribution
in the ordering temperatures. We analyzed the  SR spectra with a
functional form of:
SR spectra with a
functional form of:
| 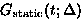 |
(4) |
where 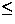 is the paramagnetic volume fraction in the sample
and
is the paramagnetic volume fraction in the sample
and 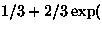 is the static Gaussian Kubo-Toyabe
function at T
is the static Gaussian Kubo-Toyabe
function at T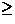 30 K or a static Gaussian function
(
30 K or a static Gaussian function
(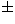 )) at T
)) at T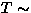 40 K. The parameter
40 K. The parameter
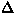 is the Gaussian field distribution width, which is
proportional to the size of the ordered Cu moments. At
T
is the Gaussian field distribution width, which is
proportional to the size of the ordered Cu moments. At
T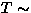 40 K,
40 K, 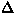 represents an `average' of the field-widths at
the muon sites. We show the temperature dependence of
represents an `average' of the field-widths at
the muon sites. We show the temperature dependence of 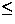 and
and 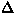 in Fig.29b. The ordering
temperature is around 52 K with a distribution of
in Fig.29b. The ordering
temperature is around 52 K with a distribution of  5 K, as deduced
from the temperature dependence of
5 K, as deduced
from the temperature dependence of 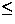 .
.




Next: Longitudinal-field measurements
Up: 4.3 SR measurements
Previous: 4.3.1 The 3-leg ladder


![]() ordered volume fraction) decreases as temperature increases
and (2) the `dip' in the spectra disappears above
ordered volume fraction) decreases as temperature increases
and (2) the `dip' in the spectra disappears above ![]() 40 K, although
the relaxation is static as shown by the decay to the 1/3-component.
The absence of the dip in the static relaxation suggests a
distribution of the field-widths (
40 K, although
the relaxation is static as shown by the decay to the 1/3-component.
The absence of the dip in the static relaxation suggests a
distribution of the field-widths (![]() ), which would result from a distribution
in the ordering temperatures. We analyzed the
), which would result from a distribution
in the ordering temperatures. We analyzed the ![]() SR spectra with a
functional form of:
SR spectra with a
functional form of: