3.1 Gaussian Kubo-Toyabe theory [#!Toyabe66!#,#!KuboToyabe67!#,#!HayanoPRB79!#]

 A conventional spin relaxation theory in zero and low external fields (Kubo-Toyabe theory [4,5,6]) begins with the assumption that there are no fluctuations in the spin system. In this static situation, each muon detects a local field (${\mbox{\boldmath$H$\unboldmath}}_{\rm loc}$) which causes Larmor precession of the muon spin (Fig.15). The time evolution of the muon spin in the static local field behaves as:

where $\theta$ is the angle between the static local field (${\mbox{\boldmath$H$\unboldmath}}_{\rm loc}$) and the initial muon spin direction (${\mbox{\boldmath$S$\unboldmath}}_{\mu}(t=0)$), and $\gamma_{\mu}$ is the gyromagnetic ratio of the muon spin (=2$\pi\times$13.554 kHz/G). Hereafter, the z-axis is defined to be the direction of the initial muon spin polarization.

  

Figure 15: Larmor precession of a muon spin in a static local field $H_{\rm loc}$.

When the local field has a distribution $\rho({\mbox{\boldmath$H$\unboldmath}})$, the muon spin relaxation observed is the ensemble average of the individual muon spin precession:

If the field distribution is isotropic, or the measurement is done on a polycrystalline specimen, one can integrate the angular part:

The first term (1/3-component) originates from the fraction of the local field which is parallel to the initial muon spin polarization. This term is an important signature of static relaxation, because its existence doesn't depend on the shape of the field distribution. The second term (2/3-component) is the Fourier transform of the field distribution, and hence, contains all information about $\rho(H)$.

  

Figure 16: Randomly oriented dense spin system. The local field is well approximated with an isotropic Gaussian distribution.

In a randomly oriented frozen spin system, with a static moment at every lattice point (Fig.16), the dipolar field at a muon site is well approximated by an isotropic Gaussian distribution:

where 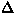$\Delta$ is the width of the Gaussian distribution. The corresponding muon spin relaxation is derived by performing the integral:

This result, known as the `static Gaussian Kubo-Toyabe function' in zero-field, was first derived by R. Kubo and T. Toyabe in 1966 [4,5].

As shown later in this chapter, it is important to investigate the muon spin relaxation in a `longitudinal field', which is the external magnetic field applied parallel to the initial muon spin polarization (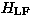$H_{\rm LF}$; see Fig.15). The static Gaussian Kubo-Toyabe function in longitudinal fields is expressed as [6]:

In Fig.17, the static Gaussian Kubo-Toyabe function $G^{\rm GKT}(t; \Delta, H_{\rm LF})$ is shown for various longitudinal fields. In zero magnetic field, the function first decays as a Gaussian and then comes back up to the non-relaxing 1/3-component. With a longitudinal field applied, the amplitude of the flat component increases, because the fraction of the field which is parallel to the initial muon spin polarization increases. In static relaxation, the magnitude of the longitudinal field which decouples the relaxation is comparable to the field distribution width ($H_{\rm LF}\sim\Delta/\gamma_\mu$). The distribution width can also be extracted from the Gaussian decay-rate at early times before the recovery.

  

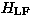Figure 17: The muon spin relaxation in the randomly oriented frozen dense spin system: static Gaussian Kubo-Toyabe function $G^{\rm GKT}(t; \Delta, H_{\rm LF})$.The circle in the figure represents the isotropic random field distribution, which is centered at zero in zero external field; if the longitudinal field ($H_{\rm LF}$) is applied, the random field is centered at $H_{\rm LF}$.

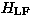Experimentally, the Gaussian Kubo-Toyabe behavior of the muon spin relaxation, as well as its longitudinal field dependence, is typically observed in substances with nuclear magnetic moments, such as MnSi [6] and copper [35].