



Next: 3.2 Lorentzian theory [#!UemuraPRB85!#]
Up: 3.1 Gaussian Kubo-Toyabe theory
Previous: 3.1 Gaussian Kubo-Toyabe theory
In the framework of the Kubo-Toyabe theory, the effects of field
fluctuations have been taken into account with the `strong collision
model' [36,6]. This model assumes that (1)
fluctuations occur suddenly, and that (2) every time the local field
fluctuates, the muon forgets the previous local field information.
Hereafter, the field fluctuation rate (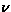 ) is defined as the
Markoffian fluctuation rate, namely, the exponential decay rate
of the autocorrelation function of the local fields:
) is defined as the
Markoffian fluctuation rate, namely, the exponential decay rate
of the autocorrelation function of the local fields:
The strong collision model generally calculates the dynamical muon spin
relaxation 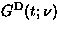 from the original static relaxation function
G(t) as follows:
from the original static relaxation function
G(t) as follows:
The terms of this series account for the muons which experienced 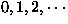 field fluctuations in the time interval of
field fluctuations in the time interval of 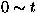 .
.
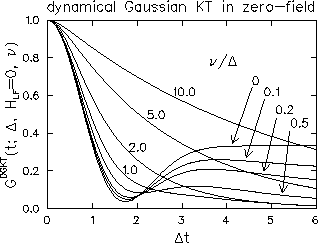
Fig.18 shows the dynamical Gaussian Kubo-Toyabe
function in zero-field for various fluctuation rates (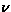 ).
In the slow fluctuation regime (
).
In the slow fluctuation regime (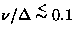 ), the
fluctuation induces slow relaxation of the 1/3-component. The
asymptotic behavior of this relaxation has been obtained as
), the
fluctuation induces slow relaxation of the 1/3-component. The
asymptotic behavior of this relaxation has been obtained as 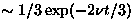 [6]. In the intermediate
fluctuation regime (
[6]. In the intermediate
fluctuation regime ( ), the
relaxation has a Gaussian behavior in the beginning, but loses
the 1/3-component. Hence, the existence/absence of the 1/3-component
is a clue which distinguishes static/dynamic relaxation.
), the
relaxation has a Gaussian behavior in the beginning, but loses
the 1/3-component. Hence, the existence/absence of the 1/3-component
is a clue which distinguishes static/dynamic relaxation.
Figure 18:
The zero-field muon spin relaxation in the fluctuating Gaussian local field
(dynamical Gaussian Kubo-Toyabe function 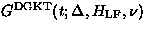 ).
).
 |
In the fast fluctuation regime (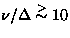 ), the relaxation is
approximated by an exponential function [7,37]:
), the relaxation is
approximated by an exponential function [7,37]:
where the relaxation rate is:
In this fast fluctuation regime, the relaxation rate (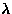 )decreases with faster fluctuation rates. This phenomenon is known as the
`motional narrowing' of the T1 relaxation rate.
The longitudinal field dependence of the relaxation rate (
)decreases with faster fluctuation rates. This phenomenon is known as the
`motional narrowing' of the T1 relaxation rate.
The longitudinal field dependence of the relaxation rate (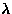 )is consistent with that of the T1 relaxation theory
[34], which has been developed for nuclear
magnetic resonance (NMR).
)is consistent with that of the T1 relaxation theory
[34], which has been developed for nuclear
magnetic resonance (NMR).




Next: 3.2 Lorentzian theory [#!UemuraPRB85!#]
Up: 3.1 Gaussian Kubo-Toyabe theory
Previous: 3.1 Gaussian Kubo-Toyabe theory
![]() ).
In the slow fluctuation regime (
).
In the slow fluctuation regime (![]() ), the
fluctuation induces slow relaxation of the 1/3-component. The
asymptotic behavior of this relaxation has been obtained as
), the
fluctuation induces slow relaxation of the 1/3-component. The
asymptotic behavior of this relaxation has been obtained as ![]() [6]. In the intermediate
fluctuation regime (
[6]. In the intermediate
fluctuation regime (![]() ), the
relaxation has a Gaussian behavior in the beginning, but loses
the 1/3-component. Hence, the existence/absence of the 1/3-component
is a clue which distinguishes static/dynamic relaxation.
), the
relaxation has a Gaussian behavior in the beginning, but loses
the 1/3-component. Hence, the existence/absence of the 1/3-component
is a clue which distinguishes static/dynamic relaxation.

![]() ), the relaxation is
approximated by an exponential function [7,37]:
), the relaxation is
approximated by an exponential function [7,37]: