The Measured Asymmetry

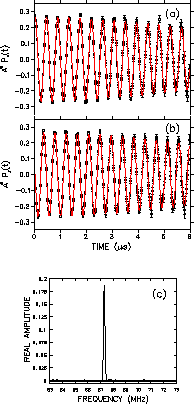
Transverse-field $\mu ^{+}$SR spectra with approximately $2 \times 10^{7}$muon decay events were taken under conditions of field cooling in applied magnetic fields of 0.5T and 1.5T. Figure 4.2(a) and Fig. 4.2(b) show the real and imaginary asymmetry spectra pertaining to the $\mbox{YBa$_{2}$ Cu$_{3}$ O$_{6.95}$ }$ sample resting in an applied field of 0.5T and at a temperature well above T_c ( i.e. $T \approx 110$K). For convenience the signals are displayed in a reference frame rotating at a frequency 2.3MHz below the Larmor precession frequency of a free muon. The average frequency of oscillation in Fig. 4.2(a) and Fig. 4.2(b) is determined by the applied magnetic field of 0.5T. Consequently, the corresponding frequency distribution [see Fig. 4.2(c)] exhibits a single peak at 67.3MHz related to the applied field through Eq. (3.14). Visual inspection of Fig. 4.2(a) and Fig. 4.2(b) suggests that the real and imaginary asymmetry spectra differ in phase by $90^{\circ}$, consistent with the discussion in the previous chapter. The solid curve passing through the data points is a fit to the data using a polarization function in the form of Eq. (3.21) with a relaxation function resembling Eq. (3.33), so that

$$A(t) = A^{\circ} P(t) = A^{\circ}_{ns} e^{- \sigma_{ns}^{2} t^{2} /2} cos \left( 2 \pi \nu_{\mu}t + \theta \right)$$ (1)

where $A^{\circ}_{ns}$ (ns $\equiv$ normal state) is the precession amplitude, $\sigma_{ns}$is the depolarization rate due to nuclear dipolar broadening and $\nu_{\mu}$ is the average precession frequency of a muon about the applied magnetic field. The real and imaginary parts of the measured asymmetry were fit simultaneously. The relaxation of the muon spin precession signal is small and is owing primarily to the distribution of the nuclear-dipolar fields in the sample. In particular, $\sigma_{ns} \approx 0.13 \mu \mbox{s}^{-1}$ in Fig. 4.2.

  

Figure 4.2: (a) The real part and, (b) the imaginary part of the muon precession signal in $\mbox{YBa$_{2}$ Cu$_{3}$ O$_{6.95}$ }$ at 110K in a magnetic field of 0.5T. The solid curves are a fit to the data assuming a gaussian distribution of fields [see Eq. (4.1)]. (c) The corresponding frequency distribution. The peak is at 67.31MHz, corresponding to an average field of 0.497T.

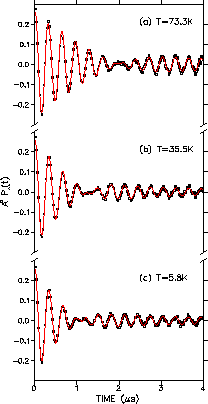
As one cools the sample below T_c, the relaxation rate of the muon precession signal increases due to the presence of the vortex lattice. The asymmetry spectra pertaining to a pair of counters for the $\mbox{YBa$_{2}$ Cu$_{3}$ O$_{6.95}$ }$crystals in an applied field of 0.5T is shown for three different temperatures below T_cin Fig. 4.3. The signals are shown in a rotating reference frame 3.3MHz below the Larmor precession frequency of a free muon. As the muons stop randomly on the length scale of the flux lattice, the muon spin precession signal provides a random sampling of the internal field distribution in the vortex state. The ensuing asymmetry spectrum is a superposition of a signal resembling Fig. 3.12 originating from muons which stop in the sample and an inseparable background signal resembling Fig. 4.2(c), due to muons which miss the sample, do not trigger the veto counter and whose positron also does not trigger the veto counter. The origin of the residual background signal is still uncertain, but may be due to those muons which scatter at wide angles after passing through the muon counter and are thus not vetoed by the V counter. Fig. 3.12 was obtained by choosing a rotating reference frame frequency equal to the background frequency, determined by fitting the data. Unfortunately, the broadening of the background signal is not necessarily identical to the field distribution above T_c and thus cannot be fixed in the fits below T_c.

  

Figure 4.3: The muon precession signal for $\mbox{YBa$_{2}$ Cu$_{3}$ O$_{6.95}$ }$ in a field of 0.5T and at, (a) 73.3K, (b) 35.5K and (c) 5.8K. The solid curves are a fit to the data assuming the field distribution of Eq. (2.10).

  

Figure 4.4: The corresponding Fourier transforms of Fig. 4.3 for $\mbox{YBa$_{2}$ Cu$_{3}$ O$_{6.95}$ }$ in a field of 0.5T and at, (a) 73.3K, (b) 35.5K and (c) 5.8K.

The beat occurring in all three spectra of Fig. 4.3 is due to the difference in the average precession frequency of a muon in the internal field of the vortex lattice and the precession frequency of the muon in the background field. The solid curves in Fig. 4.3 are fits to the theoretical polarization function of Eq. (3.39). An additional polarization function in the form of Eq. (4.1) was added to model the background signal pertaining to the muons which missed the sample, so that the measured asymmetry is of the form:

A(t) = A_sam (t) + A_bkg (t) (2)

where A_sam (t) (sam $\equiv$ sample) is as given in Eq. (3.39) and the background asymmetry A_bkg (t) (bkg $\equiv$ background) has the form:

$$A_{bkg} (t) = A^{\circ}_{bkg}e^{- \sigma^{2}_{bkg} t^{2} /2} \cos \left( \gamma_{\mu} \overline{B}_{bkg}\, t + \theta \right)$$ (3)

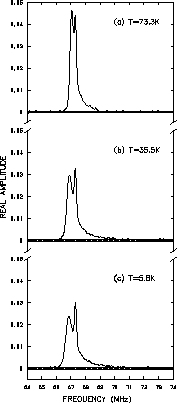
As the temperature is lowered, the vortices become better separated and the muon spin relaxes faster due to the presence of a broader distribution of internal magnetic fields. This is better displayed in Fig. 4.4 which shows the corresponding real Fourier transforms of Fig. 4.3. Recall from Eq. (3.6) that the width of the field distribution is proportional to $1/ \lambda_{ab}^{2} (T)$. Thus it is clear from Fig. 4.4 that $\lambda _{ab} (T)$ decreases with decreasing temperature. The sharp spike on the right side of each frequency distribution in Fig. 4.4 is attributed to the residual background signal. It has been determined to account for approximately $13 \%$of the total signal amplitude at 0.5T and $\sim 5 \%$ at 1.5T.

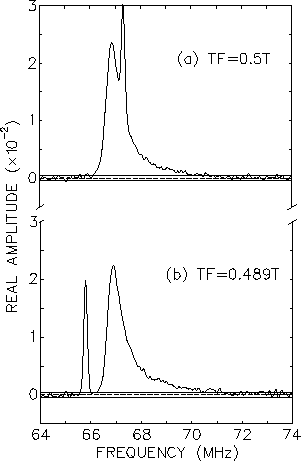
Figure 4.5 shows the frequency distribution resulting from field cooling the sample in the 0.5T field [Fig. 4.5(a)] and then lowering the applied field by 11.3mT [Fig. 4.5(b)]. As shown the background signal shifts down by 1.5MHz and positions itself at the Larmor frequency corresponding to the new applied field. The signal originating from muons which stop in the sample does not appear to change under this small shift in field. This clearly demonstrates that at low temperatures the vortex lattice is strongly pinned. Furthermore, the absence of any background peak in the unshifted signal implies that the sample is free of any appreciable non-superconducting inclusions. The shifting of the background peak away from the sample signal has since been duplicated for higher temperatures and at other applied fields. Field shifts in excess of $\sim 200$G were not attempted for fear that the crystals would shatter as a result of the strain exerted by the pinned vortex lattice.

  

Figure 4.5: (a) The Fourier transform of Fig. 4.3(c) [ i.e. the same as Fig. 4.4(c)] for $\mbox{YBa$_{2}$ Cu$_{3}$ O$_{6.95}$ }$ in a field of 0.5T at 5.8K. (b) Same as in (a) except that the field was lowered by 11.3mT after field cooling to 6K.

The asymmetric frequency distribution shown isolated in Fig. 4.5(b) has the basic features one would anticipate for a triangular vortex lattice, but with the van Hove singularities shown in Fig. 3.1(b) smeared out. Structural defects in the vortex lattice, variations in the average field due to demagnetization effects and $\vec{a}$-$\vec{b}$ anisotropy are all possible reasons for a lack of sharper features.