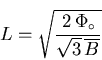


Next: 4-Counter Geometry and the Complex Polarization
Up: Measuring the penetration depth with TF-SR
Previous: The Relaxation Function
In terms of 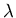 ,
the experimental raw asymmetry for TF-
,
the experimental raw asymmetry for TF- SR
analysis of the vortex state in an isotropic type-II superconductor
can be modelled assuming that the contribution to A(t) from a particular
point in the flux lattice is
SR
analysis of the vortex state in an isotropic type-II superconductor
can be modelled assuming that the contribution to A(t) from a particular
point in the flux lattice is
![\begin{displaymath}A^{th}_{raw}(t) = \frac{A^{\circ}}{N} \sum_{i=1}^{N} \cos \le . . .
. . . \, \frac{K^{2} \lambda^{2}}{(1-b)}} \right] + \theta \right\}
\end{displaymath}](img288.gif) |
(35) |
where I have combined
Eqs. (3.9), (3.27) and (3.31).
Eq. (3.35) applies to an ideal flux lattice. To account
for smearing of the field distribution due to flux-lattice disorder and
nuclear dipolar fields, Eq. (3.35) must be convoluted with
a gaussian distribution in the form of Eq. (3.34):
![\begin{displaymath}A^{th}_{raw}(t) = \frac{A^{\circ}}{N}
e^{- \sigma_{eff}^{2} . . .
. . . \, \frac{K^{2} \lambda^{2}}{(1-b)}} \right] + \theta \right\}
\end{displaymath}](img289.gif) |
(36) |
Assuming that the flux-line lattice is composed of
equilateral triangles as depicted in Fig. 3.1(a), an arbitrary
reciprocal-lattice vector
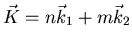 can
be written in terms of the real lattice vectors
can
be written in terms of the real lattice vectors
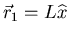 and
and
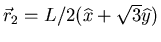 so that
so that
![\begin{displaymath}\vec{K} = \frac{2 \pi}{L} \left[ n \widehat{x} + \frac{1}{\sqrt{3}} (2m-n)
\widehat{y} \right]
\end{displaymath}](img293.gif) |
(37) |
where
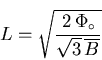 |
(38) |
is the distance between adjacent vortices. Combining Eqs. (3.36)
and (3.37) gives
 |
|
|
|
![$\displaystyle \times
\cos \left\{
\left[ \gamma_{\mu} \overline{B} t \sum_{n,m} . . .
. . . L} \right)^2 (n^{2} + m^{2}
-mn) \lambda^{2}}{(1-b)}} \right]
+ \theta \right\}$](img296.gif) |
|
|
(39) |
where
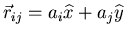 is a vector in
real space and the sum over ai and aj extends over a single
unit cell.
Eq. (3.39) can be substituted into
Eq. (3.30) and the resulting theoretical corrected
asymmetry used to fit the measured asymmetry.
is a vector in
real space and the sum over ai and aj extends over a single
unit cell.
Eq. (3.39) can be substituted into
Eq. (3.30) and the resulting theoretical corrected
asymmetry used to fit the measured asymmetry.



Next: 4-Counter Geometry and the Complex Polarization
Up: Measuring the penetration depth with TF-SR
Previous: The Relaxation Function
Jess H. Brewer
2001-09-28
![]() ,
the experimental raw asymmetry for TF-
,
the experimental raw asymmetry for TF-![]() SR
analysis of the vortex state in an isotropic type-II superconductor
can be modelled assuming that the contribution to A(t) from a particular
point in the flux lattice is
SR
analysis of the vortex state in an isotropic type-II superconductor
can be modelled assuming that the contribution to A(t) from a particular
point in the flux lattice is