


Next: The Raw Asymmetry For 2-Counter Geometry
Up: Measuring the penetration depth with TF-SR
Previous: The Field Distribution
The elegance of the 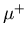 SR technique is the employment of a positive
muon
SR technique is the employment of a positive
muon 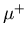 to microscopically probe the local magnetic field distribution
of Eq. (3.1) in the bulk of the superconducting sample.
Thus, measurements of the penetration depth using
to microscopically probe the local magnetic field distribution
of Eq. (3.1) in the bulk of the superconducting sample.
Thus, measurements of the penetration depth using 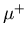 SR
are less sensitive to the
sample's surface than other conventional techniques which
measure
SR
are less sensitive to the
sample's surface than other conventional techniques which
measure 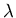 .
A positive muon has the following
properties [77,79]:
.
A positive muon has the following
properties [77,79]:
Rest mass:
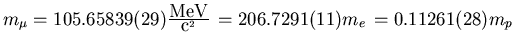
Charge: +e
Spin:
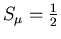
Magnetic Moment:
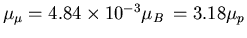
Average Lifetime:
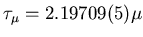 s
s
Muon Gyromagnetic Ratio:
 (
(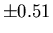 ppm)
ppm)
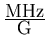
Muons are generated via the weak decay of pions:
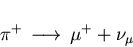 |
(12) |
A low energy 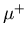 -beam can be created by
making use of the fact that some of the pions which are produced in
collisions of high energy protons with a fixed carbon or
beryllium production target
stop inside that target.
These pions rapidly decay (
-beam can be created by
making use of the fact that some of the pions which are produced in
collisions of high energy protons with a fixed carbon or
beryllium production target
stop inside that target.
These pions rapidly decay (
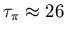 ns) according to Eq. (3.12).
Muons produced in this manner are often referred to as surface muons
to distinguish them from higher momentum muons which are obtained
from pions which decay while in flight. A
ns) according to Eq. (3.12).
Muons produced in this manner are often referred to as surface muons
to distinguish them from higher momentum muons which are obtained
from pions which decay while in flight. A 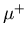 emerging from
emerging from
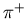 -decay has the direction of its spin antiparallel to its momentum
vector. This result follows from conservation of linear and angular
momentum, and the fact that the neutrino
-decay has the direction of its spin antiparallel to its momentum
vector. This result follows from conservation of linear and angular
momentum, and the fact that the neutrino 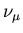 is a left-handed
particle (i.e. the neutrino helicity = -1).
A beamline composed of magnetic dipole and quadrupole magnets is used to
collect muons emitted in a given direction. Consequently, these muons are
nearly
is a left-handed
particle (i.e. the neutrino helicity = -1).
A beamline composed of magnetic dipole and quadrupole magnets is used to
collect muons emitted in a given direction. Consequently, these muons are
nearly 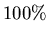 spin polarized,
with
their spin pointing backwards relative to their momentum.
spin polarized,
with
their spin pointing backwards relative to their momentum.
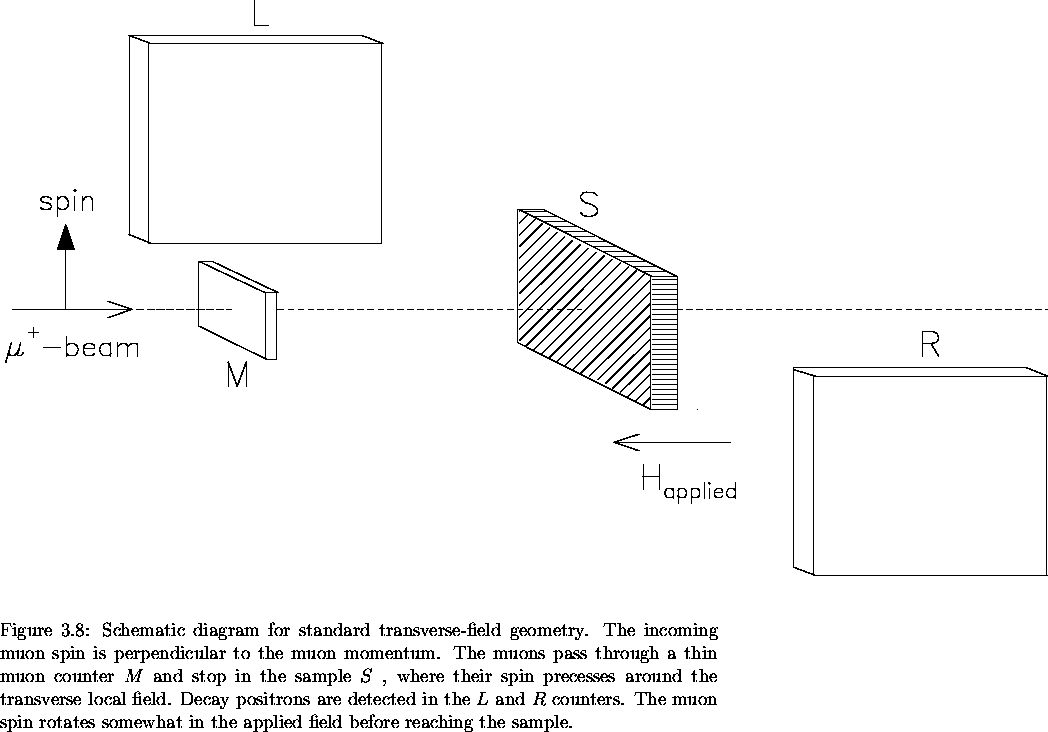
In the TF-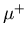 SR arrangement (see Fig. 3.10),
the
SR arrangement (see Fig. 3.10),
the 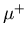 spin
is rotated perpendicular to the muon momentum using a Wien filter or
separator, which consists of mutually
perpendicular electric and magnetic fields, both of
which are transverse to the beam direction.
After passing through a collimator,
the spin-polarized positive muons are implanted
one by one into the sample, which is situated in an external field H.
The applied field is transverse to the initial muon spin
polarization, and hence parallel to the muon momentum. The muons entering the
sample rapidly thermalize (stop) within
spin
is rotated perpendicular to the muon momentum using a Wien filter or
separator, which consists of mutually
perpendicular electric and magnetic fields, both of
which are transverse to the beam direction.
After passing through a collimator,
the spin-polarized positive muons are implanted
one by one into the sample, which is situated in an external field H.
The applied field is transverse to the initial muon spin
polarization, and hence parallel to the muon momentum. The muons entering the
sample rapidly thermalize (stop) within
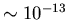 s. Their low momentum
implies a short range in the sample:
s. Their low momentum
implies a short range in the sample:
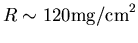 ,
which corresponds to a
thickness of approximately
,
which corresponds to a
thickness of approximately 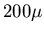 m in
m in
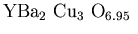 [77].
[77].
Inside the sample, the muon's magnetic moment comes under the influence
of the local magnetic field. For
 ,
the local magnetic
field
,
the local magnetic
field
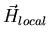 is the vector sum of the externally applied field
is the vector sum of the externally applied field
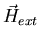 ,
the magnetic field produced by the circulating supercurrents
,
the magnetic field produced by the circulating supercurrents
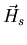 ,
and the field
,
and the field
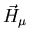 resulting from local magnetic
moments:
resulting from local magnetic
moments:
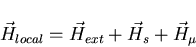 |
(13) |
The muons precess about the local field
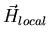 with a Larmor
frequency:
with a Larmor
frequency:
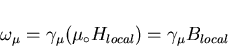 |
(14) |
where Blocal is the local magnetic induction and
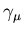 is the muon gyromagnetic ratio.
If the muons occupy
identical sites in the sample, they will be subjected to the same local magnetic
field. Therefore they will precess in phase with one another so that the
magnitude of their initial polarization is retained.
If, however, the muons
experience different magnetic fields in the sample, they will not precess
at the same Larmor frequency. The
resulting dephasing of their spins
manifests itself in a corresponding loss of polarization. After a mean lifetime
is the muon gyromagnetic ratio.
If the muons occupy
identical sites in the sample, they will be subjected to the same local magnetic
field. Therefore they will precess in phase with one another so that the
magnitude of their initial polarization is retained.
If, however, the muons
experience different magnetic fields in the sample, they will not precess
at the same Larmor frequency. The
resulting dephasing of their spins
manifests itself in a corresponding loss of polarization. After a mean lifetime
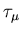 ,
the
,
the 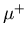 decays into a positron and two neutrinos:
decays into a positron and two neutrinos:
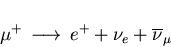 |
(15) |
The distribution of decay positrons is asymmetric with respect to the
spin polarization vector
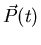 of the muon, such that the highest
probability of emission is along the direction of the muon spin.
Consequently, the time evolution of the muon spin polarization
of the muon, such that the highest
probability of emission is along the direction of the muon spin.
Consequently, the time evolution of the muon spin polarization
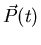 can be monitored,
since the
can be monitored,
since the 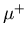 reveals its spin direction at the time of decay.
reveals its spin direction at the time of decay.
A thin 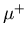 -detector placed in front of the sample registers the arrival
of a muon in the sample and starts a clock. A pair of positron detectors
(one on either side of the sample as in Fig. 3.10) can be used to detect
the positrons emerging from the
-detector placed in front of the sample registers the arrival
of a muon in the sample and starts a clock. A pair of positron detectors
(one on either side of the sample as in Fig. 3.10) can be used to detect
the positrons emerging from the 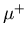 -decay. Once a decay positron is
registered, the clock is stopped. For a single
counter the number of positrons recorded per time bin
-decay. Once a decay positron is
registered, the clock is stopped. For a single
counter the number of positrons recorded per time bin 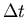 is
is
![\begin{displaymath}N(t) = N^{\circ} e^{-t/ \tau_{\mu}} \left[ 1 + A^{\circ}P(t) \right] + B^{\circ}
\end{displaymath}](img248.gif) |
(16) |
where 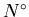 is a normalization constant,
is a normalization constant,
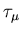 is the muon
lifetime,
is the muon
lifetime,  is the maximum precession
amplitude (or maximum experimental
decay asymmetry), P(t) is the time evolution of the
muon spin polarization in the direction of the positron counter
and
is the maximum precession
amplitude (or maximum experimental
decay asymmetry), P(t) is the time evolution of the
muon spin polarization in the direction of the positron counter
and 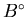 is a time-independent
background from unwanted events.
is a time-independent
background from unwanted events.



Next: The Raw Asymmetry For 2-Counter Geometry
Up: Measuring the penetration depth with TF-SR
Previous: The Field Distribution
Jess H. Brewer
2001-09-28
![]() SR technique is the employment of a positive
muon
SR technique is the employment of a positive
muon ![]() to microscopically probe the local magnetic field distribution
of Eq. (3.1) in the bulk of the superconducting sample.
Thus, measurements of the penetration depth using
to microscopically probe the local magnetic field distribution
of Eq. (3.1) in the bulk of the superconducting sample.
Thus, measurements of the penetration depth using ![]() SR
are less sensitive to the
sample's surface than other conventional techniques which
measure
SR
are less sensitive to the
sample's surface than other conventional techniques which
measure ![]() .
A positive muon has the following
properties [77,79]:
.
A positive muon has the following
properties [77,79]:
![]()
![]()
![]()
![]() s
s ![]() (
(![]() ppm)
ppm)
![]()
![]() SR arrangement (see Fig. 3.10),
the
SR arrangement (see Fig. 3.10),
the ![]() spin
is rotated perpendicular to the muon momentum using a Wien filter or
separator, which consists of mutually
perpendicular electric and magnetic fields, both of
which are transverse to the beam direction.
After passing through a collimator,
the spin-polarized positive muons are implanted
one by one into the sample, which is situated in an external field H.
The applied field is transverse to the initial muon spin
polarization, and hence parallel to the muon momentum. The muons entering the
sample rapidly thermalize (stop) within
spin
is rotated perpendicular to the muon momentum using a Wien filter or
separator, which consists of mutually
perpendicular electric and magnetic fields, both of
which are transverse to the beam direction.
After passing through a collimator,
the spin-polarized positive muons are implanted
one by one into the sample, which is situated in an external field H.
The applied field is transverse to the initial muon spin
polarization, and hence parallel to the muon momentum. The muons entering the
sample rapidly thermalize (stop) within
![]() s. Their low momentum
implies a short range in the sample:
s. Their low momentum
implies a short range in the sample:
![]() ,
which corresponds to a
thickness of approximately
,
which corresponds to a
thickness of approximately ![]() m in
m in
![]() [77].
[77].
![]() ,
the local magnetic
field
,
the local magnetic
field
![]() is the vector sum of the externally applied field
is the vector sum of the externally applied field
![]() ,
the magnetic field produced by the circulating supercurrents
,
the magnetic field produced by the circulating supercurrents
![]() ,
and the field
,
and the field
![]() resulting from local magnetic
moments:
resulting from local magnetic
moments:
![]() -detector placed in front of the sample registers the arrival
of a muon in the sample and starts a clock. A pair of positron detectors
(one on either side of the sample as in Fig. 3.10) can be used to detect
the positrons emerging from the
-detector placed in front of the sample registers the arrival
of a muon in the sample and starts a clock. A pair of positron detectors
(one on either side of the sample as in Fig. 3.10) can be used to detect
the positrons emerging from the ![]() -decay. Once a decay positron is
registered, the clock is stopped. For a single
counter the number of positrons recorded per time bin
-decay. Once a decay positron is
registered, the clock is stopped. For a single
counter the number of positrons recorded per time bin ![]() is
is