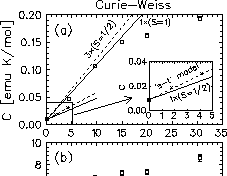
 |
 ), and fast
fluctuating otherwise (Fig.44). If the muon
spin relaxation occurs only during the slow fluctuation time, a
Gaussian relaxation rate may be observed, but with a diluted
relaxation rate as
), and fast
fluctuating otherwise (Fig.44). If the muon
spin relaxation occurs only during the slow fluctuation time, a
Gaussian relaxation rate may be observed, but with a diluted
relaxation rate as  |
Taking into account the slow paramagnetic relaxation caused during the
fast fluctuation time, the muon spin relaxation due to this unconventional
field fluctuations may be expressed as [106]:
 .
.
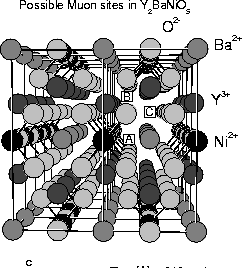 |
Using the same hypothetical relaxation function
(eq.44), we have analyzed the spectra from other
Ca-doped systems (x=4.5, 14.9 and 30.5%). The fraction parameter
(f) and the instantaneous Gaussian width (![]() ) are shown in
Fig.46. It was found that the Gaussian width
(
) are shown in
Fig.46. It was found that the Gaussian width
(![]() ) is almost independent of the Ca concentrations (x), while
the fraction parameter (f) reflects the concentrations: a smaller Ca
concentration results in a smaller fraction parameter (f),
indicating more unconventional fluctuations (note that regular
Markoffian spin fluctuations are described with f=1). The indifference
of the Gaussian width (
) is almost independent of the Ca concentrations (x), while
the fraction parameter (f) reflects the concentrations: a smaller Ca
concentration results in a smaller fraction parameter (f),
indicating more unconventional fluctuations (note that regular
Markoffian spin fluctuations are described with f=1). The indifference
of the Gaussian width (![]() ) to the charge concentrations suggests
that the muon spin relaxation mechanism is common to all the
charge doped systems, but how frequently the relaxation is caused
(
) to the charge concentrations suggests
that the muon spin relaxation mechanism is common to all the
charge doped systems, but how frequently the relaxation is caused
(![]() ) is determined by the charge concentration.
) is determined by the charge concentration.
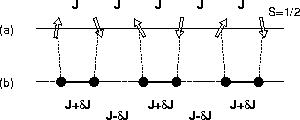 |
One possible description of the relaxation mechanism is that the doped hole, which takes a localized state with hopping [103], occasionally comes close to the muon site and induces muon spin relaxation. When the charge is far away, the muon relaxation should be small and dynamic, because the majority of the spins on the chain may stay in the non-magnetic ground state.
Phenomenologically, the magnetic behavior of the charge doped Haldane
material (Y2-xCax)BaNiO5 is very similar to that of the Kagomé-lattice
compound (SrCrzGa12-zO19), a geometrically frustrated
antiferromagnet of Cr moments (S=3/2). The susceptibility measurements
of the Kagomé-lattice system
[107,108,109] have revealed the
existence of a small portion of unpaired spins (![]() % of the
total Cr ions for the z=8 sample), which exhibit a spin-glass-like
history dependence below
% of the
total Cr ions for the z=8 sample), which exhibit a spin-glass-like
history dependence below ![]() K.
The unpaired moments observed in the susceptibilities are
probably caused by Ga substitutions to the Cr sites, which are
inevitable in this series of Kagomé compounds [109]. The
ZF-
K.
The unpaired moments observed in the susceptibilities are
probably caused by Ga substitutions to the Cr sites, which are
inevitable in this series of Kagomé compounds [109]. The
ZF-![]() SR spectrum of the z=8 Kagomé material approaches a
Gaussian shape as
SR spectrum of the z=8 Kagomé material approaches a
Gaussian shape as ![]() [106], while
LF-
[106], while
LF-![]() SR measurements at 100 mK suggest fast field fluctuations
[95,106,110]. Neutron scattering
measurements of the z=7.1 Kagomé compound [111] have
also suggested persistent dynamics below the cusp temperature; a
large fraction (
SR measurements at 100 mK suggest fast field fluctuations
[95,106,110]. Neutron scattering
measurements of the z=7.1 Kagomé compound [111] have
also suggested persistent dynamics below the cusp temperature; a
large fraction ( ) of the scattering intensity was found to
remain in the inelastic channel at
) of the scattering intensity was found to
remain in the inelastic channel at ![]() .
.
Theoretically, the S=1/2 Kagomé-lattice system may have a ground
state composed of many singlet pairs [112], as
expressed by the resonating valence bond (RVB) state. In this
situation, the unpaired spins created by non-magnetic ion doping still
have the ability to migrate spatially, because the surrounding
spins have a large number of combinations for their singlet pairings.
In the charge doped Haldane system, the doped charge may also move,
with the surrounding spins in the singlet state. Considering
these similarities, the persistent dynamics below the spin-glass like
cusp temperature, as well as the hardly decoupled Gaussian relaxation
of ![]() SR spectra may be common signatures
for migrating unpaired spins in singlet ground state materials.
SR spectra may be common signatures
for migrating unpaired spins in singlet ground state materials.