Charge doped systems

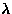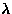In the Ca doped systems, a sharp increase of the relaxation rate ($\lambda$) was observed as the temperature approached $T_{\rm g}$ from the paramagnetic side (Fig.41). The increase of the relaxation rate probably reflects the critical slowing down of the moments, as has been observed typically in spin glass systems [7]. In the Ca doped x=4.5% sample, the temperature dependence of $\lambda$ suggests a glass temperature $T_{\rm g}\sim 1.5$ K, which was below the temperature of our SQUID magnetometer.

  

Figure 43: LF-$\mu$SR spectra in the Ca doped x=9.5% sample at 50 mK. The solid line on the zero-field (ZF) data is the fit with a dynamical Gaussian Kubo-Toyabe function. The broken line is the Kubo-Toyabe function in static case.

In order to investigate field fluctuations in the charge doped system, we performed longitudinal field measurements. The results are shown in Fig. 43. The zero-field (ZF) spectrum exhibited a Gaussian decay, which seemed to be the Gaussian Kubo-Toyabe function in the slow fluctuation regime (see section 3.1). However, the LF dependence of the relaxation didn't follow the predictions of the Gaussian Kubo-Toyabe theory. If the Gaussian behavior in the zero-field were due to almost static Gaussian field distribution, the relaxation should have been decoupled in a LF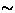$\sim$200 G, while in fact, the relaxation was present up to LF=2 kG. There are two unconventional behaviors presented in this result:

(1)

The weak LF dependence of the relaxation suggests persistent dynamics in the spin system, even though the temperature (T=50 mK) is well below the glass temperature ($T/T_{\rm g}\approx 0.02$).

(2)

There has been no theories which allow the coexistence of the zero-field Gaussian decay and fast field fluctuations. In the framework of the conventional Kubo-Toyabe theory, fast fluctuation induces either an exponential function (dense spin system) or a square-root exponential function (dilute spin system), but never a Gaussian decay (see Chapter 3).

This result is further investigated in the next section.