



Next: Nominally pure and the
Up: 5.2 Haldane material YBaNiO
Previous: 5.2.1 Susceptibility measurements
Fig. 40a shows the  SR spectra
of the nominally pure (x=y=0) system. There was slow
relaxation in zero-field (ZF, 2.8 K), but the relaxation did not disappear
in an external longitudinal field (LF=100 G). This LF measurement
proves that the relaxation is in the fast fluctuation regime; if the slow
relaxation in zero-field were due to a static random field
distribution, it should have been decoupled in a small LF
SR spectra
of the nominally pure (x=y=0) system. There was slow
relaxation in zero-field (ZF, 2.8 K), but the relaxation did not disappear
in an external longitudinal field (LF=100 G). This LF measurement
proves that the relaxation is in the fast fluctuation regime; if the slow
relaxation in zero-field were due to a static random field
distribution, it should have been decoupled in a small LF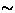 5 G
(see section 3.4).
In the nominally pure system, we have confirmed the
absence of static order down to 100 mK.
5 G
(see section 3.4).
In the nominally pure system, we have confirmed the
absence of static order down to 100 mK.
The slow relaxation of the
muon spin follows a square-root exponential function
(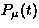

 ; solid lines in
Fig.40a), which is characteristic of
dilute spin systems in a paramagnetic state (see section
3.2). As discussed later, the slow T1 relaxation is
most likely caused by native unpaired spins in the sample.
; solid lines in
Fig.40a), which is characteristic of
dilute spin systems in a paramagnetic state (see section
3.2). As discussed later, the slow T1 relaxation is
most likely caused by native unpaired spins in the sample.
Figure 40:
(a)  SR spectra of the nominally pure Y2BaNiO5. The
solid line is the fit with the square-root exponential function. (b)
LF=100 G
SR spectra of the nominally pure Y2BaNiO5. The
solid line is the fit with the square-root exponential function. (b)
LF=100 G  SR spectra are compared at T
SR spectra are compared at T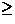 100 mK. The
solid lines are the fit with the stretched exponential functions.
100 mK. The
solid lines are the fit with the stretched exponential functions.
 |
In Fig. 40b, we compare  SR spectra from the pure, charge doped (Ca; x=4.5 and 9.5%) and
vacancy doped (Mg; y=4.1%) systems in the milli-Kelvin regime. In
the Ca doped, x=9.5% sample, there is fast muon spin relaxation, reflecting
the spin-glass behavior in the susceptibility. In the Mg doped y=4.1% sample, muon spin
relaxation is even slower than in the nominally pure system,
which suggests an absence of static order in the Mg doped systems.
This point was also confirmed with longitudinal field
decoupling measurements (Fig.42).
SR spectra from the pure, charge doped (Ca; x=4.5 and 9.5%) and
vacancy doped (Mg; y=4.1%) systems in the milli-Kelvin regime. In
the Ca doped, x=9.5% sample, there is fast muon spin relaxation, reflecting
the spin-glass behavior in the susceptibility. In the Mg doped y=4.1% sample, muon spin
relaxation is even slower than in the nominally pure system,
which suggests an absence of static order in the Mg doped systems.
This point was also confirmed with longitudinal field
decoupling measurements (Fig.42).
In order to obtain the muon spin relaxation rate (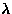 ), we analyzed
the spectra with a phenomenological stretched exponential function,
), we analyzed
the spectra with a phenomenological stretched exponential function,
 , which describes paramagnetic relaxation
with
, which describes paramagnetic relaxation
with  (see Chapter 3), as well as
the slow fluctuation regime of dilute spin systems
(
(see Chapter 3), as well as
the slow fluctuation regime of dilute spin systems
( ) and the dense spin systems (
) and the dense spin systems ( ). One
problem of this universal relaxation function is that it often shows
correlations between
). One
problem of this universal relaxation function is that it often shows
correlations between 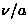 and
and 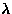 , when the relaxation rate
(
, when the relaxation rate
(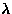 ) is small. Therefore, it is safer to fix
) is small. Therefore, it is safer to fix 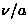 for the
analysis of the fast fluctuation regime, in order to obtain the
appropriate temperature and/or field dependence of the relaxation rate (
for the
analysis of the fast fluctuation regime, in order to obtain the
appropriate temperature and/or field dependence of the relaxation rate (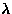 ).
).
For the analysis of the nominally pure sample, we fixed as
 , namely, to the square-root exponential function. The
overall fit was good, as shown in
Fig.40a. In the Mg-doped systems,
the
, namely, to the square-root exponential function. The
overall fit was good, as shown in
Fig.40a. In the Mg-doped systems,
the  SR spectra do not exhibit the fast front-end
(Fig.40b), suggesting
SR spectra do not exhibit the fast front-end
(Fig.40b), suggesting  .We fixed
.We fixed 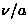 to 0.72 (Mg 1.7%) and 0.77 (Mg 4.1%) which is the
average of
to 0.72 (Mg 1.7%) and 0.77 (Mg 4.1%) which is the
average of 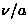 , obtained from a preceding analysis without
constraints on
, obtained from a preceding analysis without
constraints on 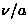 . For the Ca-doped systems at T> 6 K, we
adopted
. For the Ca-doped systems at T> 6 K, we
adopted 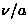 =0.5. Below 6 K, we were able to obtain
=0.5. Below 6 K, we were able to obtain 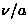 and
and
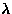 independently. It was found that
independently. It was found that 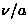 of the Ca-doped systems
approaches
of the Ca-doped systems
approaches  in the milli-Kelvin regime. In
Fig.41, relaxation rates (
in the milli-Kelvin regime. In
Fig.41, relaxation rates (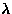 ) for
the LF=100 G measurements (and for the pure sample, the results of higher LF
measurements as well) are shown, as a function of temperature.
) for
the LF=100 G measurements (and for the pure sample, the results of higher LF
measurements as well) are shown, as a function of temperature.
Figure 41:
Temperature dependence of muon spin relaxation rate (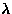 ).
For the doped samples, the results from LF=100 G measurements are shown;
for the nominally pure sample, the data in higher LF's are shown as well.
The solid lines (for the doped systems) and the dashed lines (for the
pure system) are guides to the eyes.
).
For the doped samples, the results from LF=100 G measurements are shown;
for the nominally pure sample, the data in higher LF's are shown as well.
The solid lines (for the doped systems) and the dashed lines (for the
pure system) are guides to the eyes.
 |




Next: Nominally pure and the
Up: 5.2 Haldane material YBaNiO
Previous: 5.2.1 Susceptibility measurements
![]()
![]()
![]() ; solid lines in
Fig.40a), which is characteristic of
dilute spin systems in a paramagnetic state (see section
3.2). As discussed later, the slow T1 relaxation is
most likely caused by native unpaired spins in the sample.
; solid lines in
Fig.40a), which is characteristic of
dilute spin systems in a paramagnetic state (see section
3.2). As discussed later, the slow T1 relaxation is
most likely caused by native unpaired spins in the sample.

![]() ), we analyzed
the spectra with a phenomenological stretched exponential function,
), we analyzed
the spectra with a phenomenological stretched exponential function,
![]() , which describes paramagnetic relaxation
with
, which describes paramagnetic relaxation
with ![]() (see Chapter 3), as well as
the slow fluctuation regime of dilute spin systems
(
(see Chapter 3), as well as
the slow fluctuation regime of dilute spin systems
(![]() ) and the dense spin systems (
) and the dense spin systems (![]() ). One
problem of this universal relaxation function is that it often shows
correlations between
). One
problem of this universal relaxation function is that it often shows
correlations between ![]() and
and ![]() , when the relaxation rate
(
, when the relaxation rate
(![]() ) is small. Therefore, it is safer to fix
) is small. Therefore, it is safer to fix ![]() for the
analysis of the fast fluctuation regime, in order to obtain the
appropriate temperature and/or field dependence of the relaxation rate (
for the
analysis of the fast fluctuation regime, in order to obtain the
appropriate temperature and/or field dependence of the relaxation rate (![]() ).
).
 , namely, to the square-root exponential function. The
overall fit was good, as shown in
Fig.40a. In the Mg-doped systems,
the
, namely, to the square-root exponential function. The
overall fit was good, as shown in
Fig.40a. In the Mg-doped systems,
the ![]() SR spectra do not exhibit the fast front-end
(Fig.40b), suggesting
SR spectra do not exhibit the fast front-end
(Fig.40b), suggesting ![]() .We fixed
.We fixed ![]() to 0.72 (Mg 1.7%) and 0.77 (Mg 4.1%) which is the
average of
to 0.72 (Mg 1.7%) and 0.77 (Mg 4.1%) which is the
average of ![]() , obtained from a preceding analysis without
constraints on
, obtained from a preceding analysis without
constraints on ![]() . For the Ca-doped systems at T> 6 K, we
adopted
. For the Ca-doped systems at T> 6 K, we
adopted ![]() =0.5. Below 6 K, we were able to obtain
=0.5. Below 6 K, we were able to obtain ![]() and
and
![]() independently. It was found that
independently. It was found that ![]() of the Ca-doped systems
approaches
of the Ca-doped systems
approaches  in the milli-Kelvin regime. In
Fig.41, relaxation rates (
in the milli-Kelvin regime. In
Fig.41, relaxation rates (![]() ) for
the LF=100 G measurements (and for the pure sample, the results of higher LF
measurements as well) are shown, as a function of temperature.
) for
the LF=100 G measurements (and for the pure sample, the results of higher LF
measurements as well) are shown, as a function of temperature.
