



Next: 4 Spin-ladder system
Up: 3 Spin relaxation theories
Previous: 3.3 A minor correction theory
As a concluding remark concerning the zero/low-field spin relaxation theories, I will
mention the importance of the longitudinal field measurements when
using the  SR technique as a local magnetic probe. In
Fig.24, the simulated muon spin relaxation in two different spin
systems are shown. One is a dense spin system with fast fluctuations,
and the other is a dilute spin system with slow fluctuations. In
zero-field, the two systems presents almost identical exponential
relaxation, and the two situations are indistinguishable. In longitudinal
field measurements, however, these two
systems become distinguishable. In the slowly fluctuating system, the
relaxation is decoupled with relatively small longitudinal fields,
which are comparable to the field distribution width
(Fig.24b). In the fast fluctuating system
(Fig.24a), decoupling requires much larger fields.
These qualitatively different responses to the applied longitudinal
fields allow one to experimentally distinguish between slow and fast fluctuations
of the local fields.
SR technique as a local magnetic probe. In
Fig.24, the simulated muon spin relaxation in two different spin
systems are shown. One is a dense spin system with fast fluctuations,
and the other is a dilute spin system with slow fluctuations. In
zero-field, the two systems presents almost identical exponential
relaxation, and the two situations are indistinguishable. In longitudinal
field measurements, however, these two
systems become distinguishable. In the slowly fluctuating system, the
relaxation is decoupled with relatively small longitudinal fields,
which are comparable to the field distribution width
(Fig.24b). In the fast fluctuating system
(Fig.24a), decoupling requires much larger fields.
These qualitatively different responses to the applied longitudinal
fields allow one to experimentally distinguish between slow and fast fluctuations
of the local fields.
Figure 24:
(a) Muon spin relaxation in a fast fluctuating dense spin system:
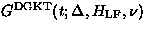 , and (b) in a slowly fluctuating
dilute spin system:
, and (b) in a slowly fluctuating
dilute spin system: 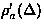 . These two
systems are distinguishable in longitudinal field measurements, but not in
zero-field.
. These two
systems are distinguishable in longitudinal field measurements, but not in
zero-field.
 |
In the following chapter, the  SR technique is applied to a
spin-ladder material, Srn-1Cun+1O2n. The set of measurements presented there
will exhibit how Kubo-Toyabe theories help us investigate the
magnetism of this material.
SR technique is applied to a
spin-ladder material, Srn-1Cun+1O2n. The set of measurements presented there
will exhibit how Kubo-Toyabe theories help us investigate the
magnetism of this material.




Next: 4 Spin-ladder system
Up: 3 Spin relaxation theories
Previous: 3.3 A minor correction theory


![]() SR technique is applied to a
spin-ladder material, Srn-1Cun+1O2n. The set of measurements presented there
will exhibit how Kubo-Toyabe theories help us investigate the
magnetism of this material.
SR technique is applied to a
spin-ladder material, Srn-1Cun+1O2n. The set of measurements presented there
will exhibit how Kubo-Toyabe theories help us investigate the
magnetism of this material.