We will restrict our attention in the following to the long-time behaviour of AC circuits; in particular, we will examine the response of circuits at the same frequency as the driving source, neglecting any transient responses.
The voltage drop across a resistor (R), capacitor (C) and inductor (L) are given as:
We can represent the current by a complex exponential:
If we now evaluate 
, 
and 
:
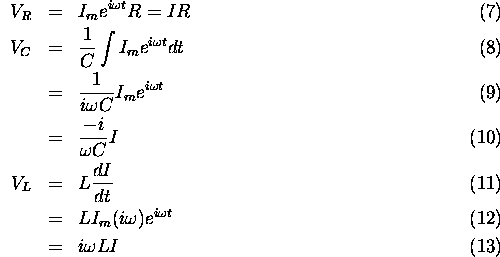
We can define the complex impedance X:
so that the voltage drop across any element is given simply as
Consider the circuit in Figure 9.6 consisting of a resistance R, a capacitance C and an inductance L, connected in series and driven by a time-varying voltage source.
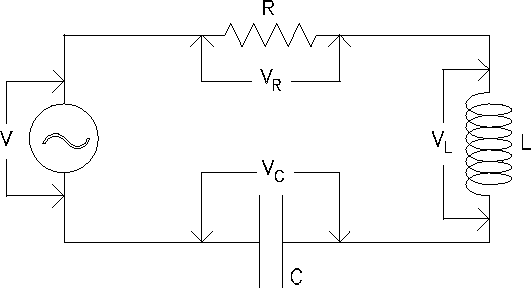
Figure 9.6: A driven series RLC circuit.
The differential equation for the current flow is obtained by equating the voltage of the source to the total potential drop around the circuit.
We write the driving sinusoidal voltage as 
, then
take the current to have the same frequency, but a relative phase 
:
To determine the response of the circuit,
we need to determine 
.
Since the left hand side of the equation for 
is purely real,
the right hand side must also be real; in other words,
the imaginary part must equal zero.
Making use of the identity
, we obtain:
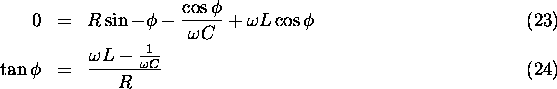
From our result for 
, we can construct a triangle
and use the Pythagorean theorem to obtain
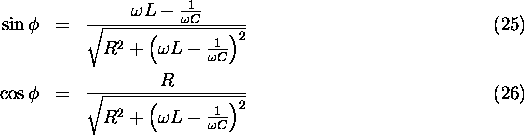
Substituting into the real part of Eq. (22) we obtain:
