Although nominally outside the terms of reference of this thesis, the following example serves to illustrate the application of the preceding theory, to clear up an historical misunderstanding and to provide continuity with recent studies of muonium diffusion.
Experiments performed by Kiefl et.al. [66]
and MacFarlane et.al. [67]
measured the muonium hop rate in KCl
over a wide temperature range, clearly showing the
position of the minimum hop rate, characteristic of the
crossover from two-phonon limited diffusion to one-phonon
activated diffusion, at ![]() K.
The measured hop rate below
K.
The measured hop rate below ![]() was fitted to a
power law relation
was fitted to a
power law relation ![]() , yielding
a value
, yielding
a value ![]() .It was noted at the time that the low temperature limiting value of
.It was noted at the time that the low temperature limiting value of
![]() predicted by theory was 7 (or 9 in a perfect fcc lattice
if the sites are symmetric with respect to the phonon modes);
the discrepancy with the measured result remained unexplained.
predicted by theory was 7 (or 9 in a perfect fcc lattice
if the sites are symmetric with respect to the phonon modes);
the discrepancy with the measured result remained unexplained.
To answer the question of why the hop rate in KCl
did not follow a T-7 dependence,
Kagan and Prokof'ev argued in their 1990 paper [54]
that if one used the real
phonon spectrum in Eq. (6.8) one could obtain agreement
with the measured T-dependence.
They wrote also in
their review article [53] that the
``experimentally found temperature dependence in this region is
considerably weaker than that predicted by the limiting law [T-7].
That is, however, associated not with the loss of the dominant role by
two-phonon processes but with the real structure of the
phonon spectrum of these crystals."
Their calculation of ![]() with the real phonon spectrum
in Eq. (6.8) obtained the result
with the real phonon spectrum
in Eq. (6.8) obtained the result ![]() .We will show here that their interpretation of the role of structure
in the phonon spectrum is not correct.
The relative weakness of the temperature dependence
(i.e. reduction of
.We will show here that their interpretation of the role of structure
in the phonon spectrum is not correct.
The relative weakness of the temperature dependence
(i.e. reduction of ![]() from 7)
is a result predicted by this theory, which would be present
even if the actual phonon spectrum were entirely Debye-like.
The structure present in the phonon density of states
of KCl is not responsible for this.
Here we will repeat the calculation performed
by Kagan and Prokof'ev, and also the case where the phonon
spectrum is a featureless, smooth Debye-like function.
from 7)
is a result predicted by this theory, which would be present
even if the actual phonon spectrum were entirely Debye-like.
The structure present in the phonon density of states
of KCl is not responsible for this.
Here we will repeat the calculation performed
by Kagan and Prokof'ev, and also the case where the phonon
spectrum is a featureless, smooth Debye-like function.
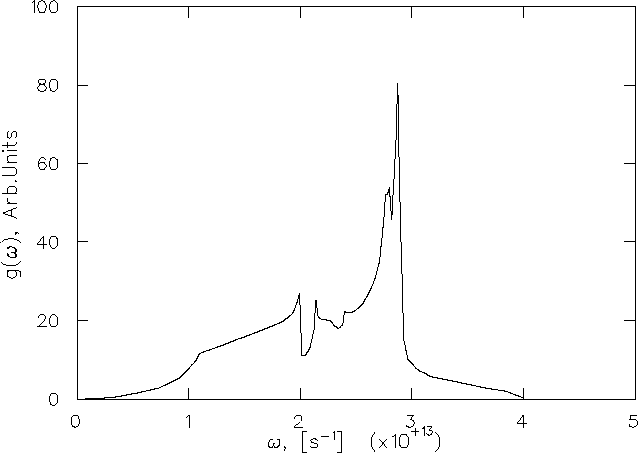
The total phonon density of states of KCl,
measured by inelastic neutron scattering [55],
is shown in Fig. 6.15.
The damping rate ![]() can then be calculated
using this spectrum for
can then be calculated
using this spectrum for ![]() in a numerical integration over phonon frequency
in a numerical integration over phonon frequency ![]() .(The Debye temperature of KCl is about 230 K, but the real phonon
density of states has its upper cut-off at
.(The Debye temperature of KCl is about 230 K, but the real phonon
density of states has its upper cut-off at
![]() .)
In this calculation,
.)
In this calculation, ![]() is normalized
so that its integral is unity,
which does not affect its T-dependence, only an overall factor.
The correct normalization of the phonon density of states can be
obtained by calculating the lattice specific heat
is normalized
so that its integral is unity,
which does not affect its T-dependence, only an overall factor.
The correct normalization of the phonon density of states can be
obtained by calculating the lattice specific heat
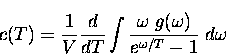 |
(10) |
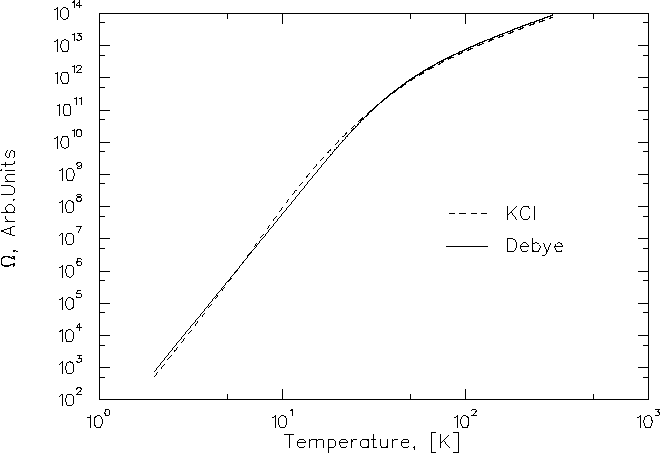
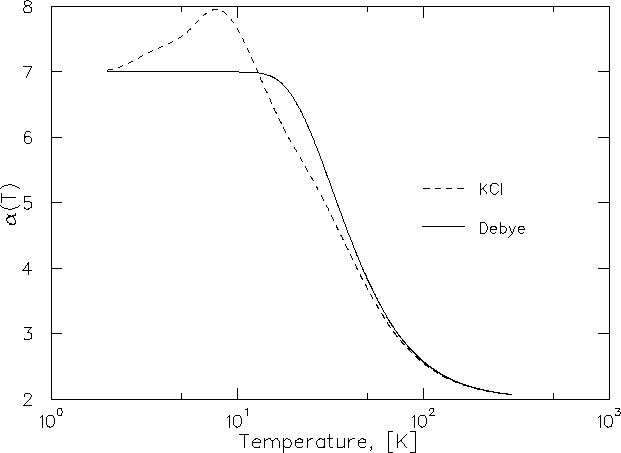
Figure 6.16 shows the temperature dependence of
![]() , along with the result obtained if it is
assumed that
, along with the result obtained if it is
assumed that ![]() .Figure 6.17 shows the temperature
dependence of the power law exponent
.Figure 6.17 shows the temperature
dependence of the power law exponent
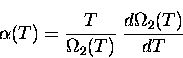
The principal cause of the weak temperature dependence of
the muonium hop rate in KCl is that the temperature where the
hop rate minimum occurs is already a sufficiently large fraction of
![]() that the entire phonon spectrum contributes to
that the entire phonon spectrum contributes to
![]() .
The population of low frequency phonons
for which
.
The population of low frequency phonons
for which ![]() increases only linearly with T;
the temperature dependence of
increases only linearly with T;
the temperature dependence of ![]() drops off.
Since the temperature at which the minimum hop rate occurs is
70 K, a substantial fraction of the Debye temperature,
we are far from the low temperature limit
where one obtains
drops off.
Since the temperature at which the minimum hop rate occurs is
70 K, a substantial fraction of the Debye temperature,
we are far from the low temperature limit
where one obtains ![]() .It can be seen from the graph that this is the case whether the real
spectrum or a Debye-like
.It can be seen from the graph that this is the case whether the real
spectrum or a Debye-like ![]() is used. It is an intrinsic
property of two-phonon diffusion, not the structure in the spectrum,
that causes
is used. It is an intrinsic
property of two-phonon diffusion, not the structure in the spectrum,
that causes ![]() to be characterized by a lower
to be characterized by a lower ![]() at temperatures greater than about
at temperatures greater than about ![]() or so.
The structure in the real
or so.
The structure in the real ![]() has a small effect on
has a small effect on ![]() , as can be seen,
but the overall shape of the function is hardly affected.
A weak temperature dependence of the 2-phonon diffusion rate
will occur in any crystal for which
, as can be seen,
but the overall shape of the function is hardly affected.
A weak temperature dependence of the 2-phonon diffusion rate
will occur in any crystal for which ![]() (the temperature
where the crossover between two-phonon and one-phonon
regimes occurs) happens to be more than
about
(the temperature
where the crossover between two-phonon and one-phonon
regimes occurs) happens to be more than
about ![]() , so that two-phonon diffusion
is important at relatively high temperatures.
Related to this, it must be stressed that the
, so that two-phonon diffusion
is important at relatively high temperatures.
Related to this, it must be stressed that the
![]() dependence is expected
only in the low temperature limit
dependence is expected
only in the low temperature limit ![]() .It is a simple exercise to show that in the high temperature limit
(several times
.It is a simple exercise to show that in the high temperature limit
(several times ![]() ),
), ![]() .At all intermediate temperatures, the characteristic exponent
.At all intermediate temperatures, the characteristic exponent ![]() is a function of temperature, and it is not very meaningful
to apply a single value to
is a function of temperature, and it is not very meaningful
to apply a single value to ![]() over a range of temperatures.
It is also possible that the coupling to
high-frequency modes doesn't
follow the simple low frequency limiting
behavior.
If this is the case, the model will fail completely at higher
temperatures.
over a range of temperatures.
It is also possible that the coupling to
high-frequency modes doesn't
follow the simple low frequency limiting
behavior.
If this is the case, the model will fail completely at higher
temperatures.
 |
 |
 |