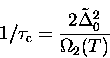


Next: 6.2 Muonium Diffusion in
Up: 6 Quantum Diffusion II:
Previous: 6 Quantum Diffusion II:
At temperatures well below the Debye temperature of the
host solid, the tunnelling diffusion rate will be determined by
the full coherent transition amplitude as long as the rate of
loss of phase coherence, 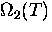 , is small compared
to the inverse of the underbarrier transition time.
Without scattering, the mean free path can exceed the lattice
constant so the particle propagates in a band-like state.
As the temperature is increased, two things happen: the enhanced
phonon population causes a very rapid increase in
, is small compared
to the inverse of the underbarrier transition time.
Without scattering, the mean free path can exceed the lattice
constant so the particle propagates in a band-like state.
As the temperature is increased, two things happen: the enhanced
phonon population causes a very rapid increase in 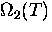 ,suppressing the coherent channel;
meanwhile the hop rate due to the one-phonon, thermally-activated
tunnelling mechanism increases exponentially.
The contribution of one-phonon hopping becomes dominant when
,suppressing the coherent channel;
meanwhile the hop rate due to the one-phonon, thermally-activated
tunnelling mechanism increases exponentially.
The contribution of one-phonon hopping becomes dominant when
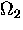 exceeds
exceeds
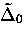 , providing a natural division
of the temperature scale.
For the purpose of discussing quantum diffusion, ``low'' temperature
means temperatures where the 2-phonon incoherent channel, though partly
diminished by phonon scattering, still exceeds the contribution
of thermally-activated hopping mediated by the one-phonon
interaction.
In this section we will consider in more detail the predictions
of theory in the incoherent regime and compare these
with experimental results.
, providing a natural division
of the temperature scale.
For the purpose of discussing quantum diffusion, ``low'' temperature
means temperatures where the 2-phonon incoherent channel, though partly
diminished by phonon scattering, still exceeds the contribution
of thermally-activated hopping mediated by the one-phonon
interaction.
In this section we will consider in more detail the predictions
of theory in the incoherent regime and compare these
with experimental results.
Previously we showed that the incoherent diffusion rate in the
presence of an interstitial-lattice coupling quadratic in
lattice displacements (i.e. two-phonon coupling) is
| 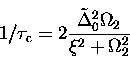 |
(1) |
where the tunnelling bandwidth renormalized by the one-phonon
interaction is
| ![\begin{displaymath}
{\tilde \Delta}_0 = \Delta_0 \exp[B_{0} - \phi(T) + G(T)]\end{displaymath}](img182.gif) |
(2) |
with 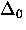 the bandwidth in a perfect lattice and
the bandwidth in a perfect lattice and 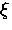 the
typical site-to-site static level shift.
The temperature dependent parameters in the exponent characterize
the polaron effect and barrier fluctuations and are respectively
the
typical site-to-site static level shift.
The temperature dependent parameters in the exponent characterize
the polaron effect and barrier fluctuations and are respectively
| 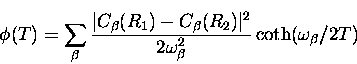 |
(3) |
and
| 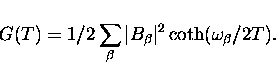 |
(4) |
The de-coherence rate 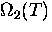 was defined in terms of the
two-phonon coupling parameters
was defined in terms of the
two-phonon coupling parameters
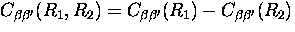 and phonon numbers
and phonon numbers 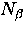 by
by
| 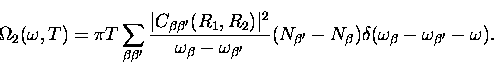 |
(5) |
Recalling that the largest contribution from phonon scattering
comes from those terms where
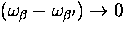 ,
we can write the difference
,
we can write the difference 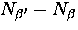 in this limit as
in this limit as
In this limit 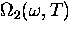 becomes frequency-independent
and is given by
becomes frequency-independent
and is given by
| 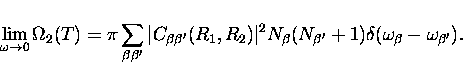 |
(6) |
Frequency independence of the damping rate 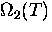 implies that two-phonon scattering is an example of
an Ohmic coupling to the medium in the Caldeira-Leggett theory
of dissipation. [38,39]
In order to obtain the hop rate as an explicit function of
temperature we approximate the summation over phonons by an
integral over the phonon density of states
implies that two-phonon scattering is an example of
an Ohmic coupling to the medium in the Caldeira-Leggett theory
of dissipation. [38,39]
In order to obtain the hop rate as an explicit function of
temperature we approximate the summation over phonons by an
integral over the phonon density of states 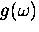
| 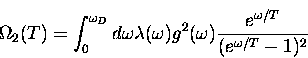 |
(7) |
where 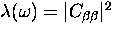 is the
matrix element in Eq. (6.5) averaged over the
branches of the phonon modes.
is the
matrix element in Eq. (6.5) averaged over the
branches of the phonon modes.
At this stage it is possible to determine the temperature
dependence of the hop rate at least qualitatively for
temperatures  .Solids generally have phonon spectra
that at long
wavelengths - the only modes excited at low T -
closely follow the Debye model
with
.Solids generally have phonon spectra
that at long
wavelengths - the only modes excited at low T -
closely follow the Debye model
with 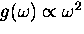 and
the coupling constant
and
the coupling constant 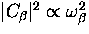 .In the low temperature limit Eq. (6.8)
then gives us
.In the low temperature limit Eq. (6.8)
then gives us 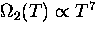 .
.
We are now in a position to consider the qualitative
temperature dependence of the interstitial diffusion rate.
In the case that 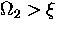 , Eq. (6.1)
reduces approximately to
, Eq. (6.1)
reduces approximately to
| 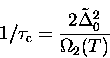 |
(8) |
and where 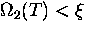 to
to
| 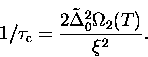 |
(9) |
Since 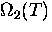 always increases monotonically with temperature
we have two possible situations.
We expect that at sufficiently low temperatures (but still large
compared to the bandwidth) there
is the possibility that Eq. (6.10) applies and
in the low temperature limit
always increases monotonically with temperature
we have two possible situations.
We expect that at sufficiently low temperatures (but still large
compared to the bandwidth) there
is the possibility that Eq. (6.10) applies and
in the low temperature limit  we have
we have 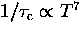 .
In this case
the scattering of phonons actually helps the diffusing
particle to overcome the static level shifts
.
In this case
the scattering of phonons actually helps the diffusing
particle to overcome the static level shifts 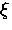 .The other possibility (generally at some higher temperature)
is that the static shifts are comparatively small
in which case Eq. (6.9) applies and
.The other possibility (generally at some higher temperature)
is that the static shifts are comparatively small
in which case Eq. (6.9) applies and
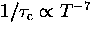 ; phonon scattering then hinders
the band-like diffusion in the periodic potential of the
lattice.
; phonon scattering then hinders
the band-like diffusion in the periodic potential of the
lattice.



Next: 6.2 Muonium Diffusion in
Up: 6 Quantum Diffusion II:
Previous: 6 Quantum Diffusion II:
![]() , is small compared
to the inverse of the underbarrier transition time.
Without scattering, the mean free path can exceed the lattice
constant so the particle propagates in a band-like state.
As the temperature is increased, two things happen: the enhanced
phonon population causes a very rapid increase in
, is small compared
to the inverse of the underbarrier transition time.
Without scattering, the mean free path can exceed the lattice
constant so the particle propagates in a band-like state.
As the temperature is increased, two things happen: the enhanced
phonon population causes a very rapid increase in ![]() ,suppressing the coherent channel;
meanwhile the hop rate due to the one-phonon, thermally-activated
tunnelling mechanism increases exponentially.
The contribution of one-phonon hopping becomes dominant when
,suppressing the coherent channel;
meanwhile the hop rate due to the one-phonon, thermally-activated
tunnelling mechanism increases exponentially.
The contribution of one-phonon hopping becomes dominant when
![]() exceeds
exceeds
![]() , providing a natural division
of the temperature scale.
For the purpose of discussing quantum diffusion, ``low'' temperature
means temperatures where the 2-phonon incoherent channel, though partly
diminished by phonon scattering, still exceeds the contribution
of thermally-activated hopping mediated by the one-phonon
interaction.
In this section we will consider in more detail the predictions
of theory in the incoherent regime and compare these
with experimental results.
, providing a natural division
of the temperature scale.
For the purpose of discussing quantum diffusion, ``low'' temperature
means temperatures where the 2-phonon incoherent channel, though partly
diminished by phonon scattering, still exceeds the contribution
of thermally-activated hopping mediated by the one-phonon
interaction.
In this section we will consider in more detail the predictions
of theory in the incoherent regime and compare these
with experimental results.
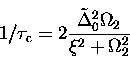
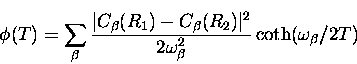
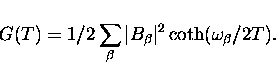
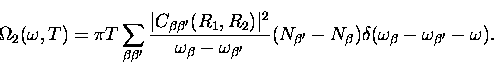
![]() ,
we can write the difference
,
we can write the difference ![]() in this limit as
in this limit as
![]() becomes frequency-independent
and is given by
becomes frequency-independent
and is given by
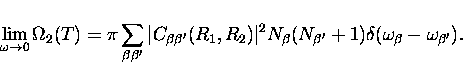
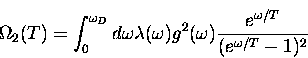
![]() .Solids generally have phonon spectra
that at long
wavelengths - the only modes excited at low T -
closely follow the Debye model
with
.Solids generally have phonon spectra
that at long
wavelengths - the only modes excited at low T -
closely follow the Debye model
with ![]() and
the coupling constant
and
the coupling constant ![]() .In the low temperature limit Eq. (6.8)
then gives us
.In the low temperature limit Eq. (6.8)
then gives us ![]() .
.![]() , Eq. (6.1)
reduces approximately to
, Eq. (6.1)
reduces approximately to