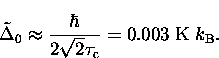


Next: 6.4 Numerical Calculations: Solid
Up: 6 Quantum Diffusion II:
Previous: 6.2 Muonium Diffusion in
In solid nitrogen muonium diffusion was studied using both
longitudinal and transverse field muon spin rotation/relaxation
techniques.
From the relaxation rates of the muon polarization
one can extract the muonium hop rate as a function of temperature.
This is compared to the behavior predicted by theory, finding
agreement at low temperatures only.
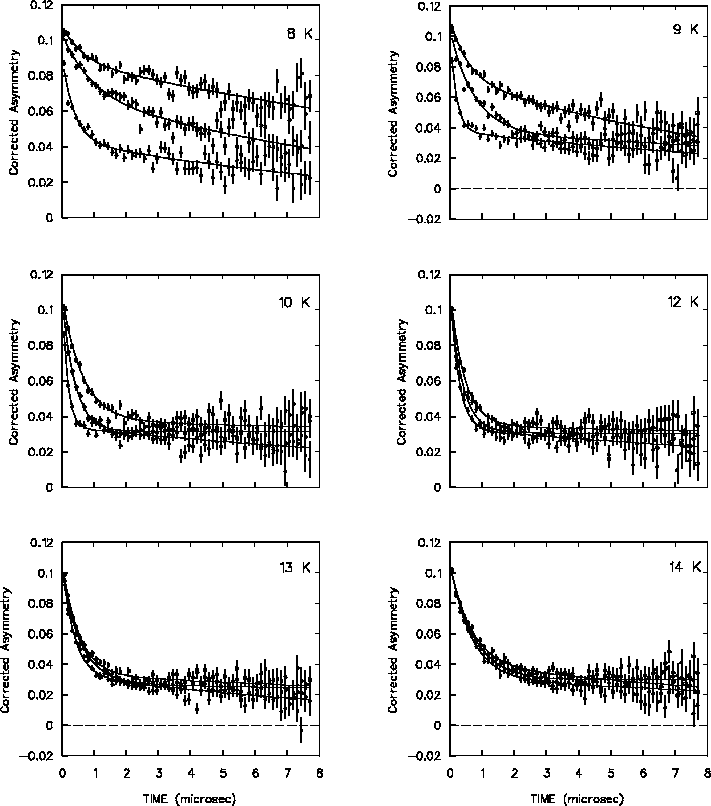
Figure 6.18:
Asymmetries measured in solid N2 at various temperatures in weak longitudinal magnetic
fields of (from bottom to top in each plot) 4, 8 and 12 G.
 |
With a weak longitudinal magnetic field of a few Gauss applied
to the sample, the muon and electron spins in muonium
are strongly coupled by the hyperfine interaction.
As the muonium atom diffuses among
atoms of the host lattice, the nuclear hyperfine (nhf) interaction
between the spins of the muonium electron and the randomly-oriented
lattice nuclear moments undergoes fluctuations.
The resulting time-dependent effective magnetic field felt
by the muonium atom excites transitions among states of the
muonium atom, and the original polarization of the muon spin
is lost.
Figure 6.18 shows the temperature and magnetic field
dependence of the muon asymmetry measured in s-N2in longitudinal field.
To a good approximation, in weak magnetic fields
the muon spin polarization
relaxes with an exponential time dependence
where the relaxation rate 1/T1 depends on the hop rate
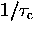 according to
according to
| 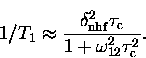 |
(12) |
Equation (6.13) also predicts the presence
of a 1/T1 maximum where 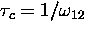 .Such maxima are evident in the relaxation rates, which peak
at different temperatures depending on the field,
allowing one to make an unambiguous determination of the
diffusion rate independent of the absolute scale
of the relaxation rate.
.Such maxima are evident in the relaxation rates, which peak
at different temperatures depending on the field,
allowing one to make an unambiguous determination of the
diffusion rate independent of the absolute scale
of the relaxation rate.
Figure 6.19 shows examples of muonium
spin precession signals measured in a weak transverse
field (wTF) of 5 G.
In weak magnetic fields the two observable muonium frequencies
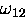 and
and 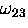 are very nearly equal
(see Appendix A for definitions of these and the other
muonium frequencies
are very nearly equal
(see Appendix A for definitions of these and the other
muonium frequencies 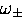 and
and 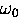 )the splitting between these two lines is
)the splitting between these two lines is
| 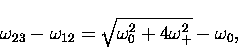 |
(13) |
and in fields 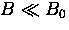 this is approximately
this is approximately
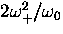 .In a transverse magnetic field of 8 G or less, and when the
muonium relaxation rate is greater than about 0.25
.In a transverse magnetic field of 8 G or less, and when the
muonium relaxation rate is greater than about 0.25 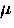 s-1,
``beating'' of the two triplet muonium frequencies is not apparent
within the 10
s-1,
``beating'' of the two triplet muonium frequencies is not apparent
within the 10 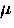 s time range of the histogram;
the muonium spin precesses with one signal
at the mean frequency
s time range of the histogram;
the muonium spin precesses with one signal
at the mean frequency
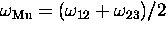 = 1.3961 MHz/G
= 1.3961 MHz/G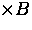 .(However, in slightly larger magnetic fields, or if the
spin relaxation rate is extremely low, the beat
envelope will masquerade
as a Gaussian relaxation function which, if one mistakenly fitted
the asymmetry with a single signal, would result in a
misleading contribution to the real relaxation rate.)
The asymmetry measured in s-N2 was fitted to a sum of
signals for fast and slowly relaxing
diamagnetic fractions and the muonium fraction:
.(However, in slightly larger magnetic fields, or if the
spin relaxation rate is extremely low, the beat
envelope will masquerade
as a Gaussian relaxation function which, if one mistakenly fitted
the asymmetry with a single signal, would result in a
misleading contribution to the real relaxation rate.)
The asymmetry measured in s-N2 was fitted to a sum of
signals for fast and slowly relaxing
diamagnetic fractions and the muonium fraction:
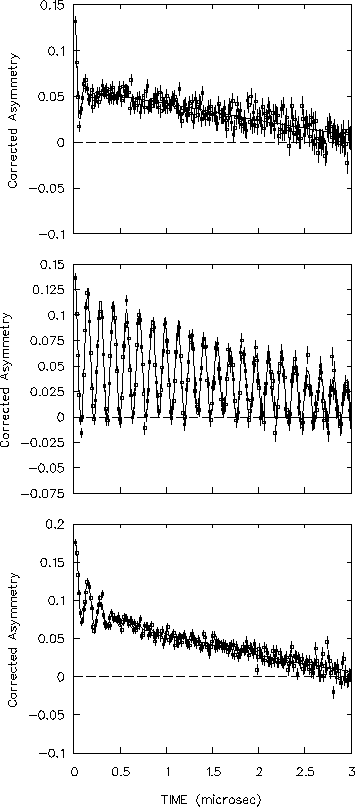
Figure 6.19:
Muon spin polarization asymmetries measured in a transverse
magnetic field of 5.2 G at temperatures of, from top to bottom,
T=3.45, 19 and 54 K in a sample of solid, pure N2.
 |
In transverse field the polarization relaxation function
depends on the particle hop rate due to the motional
narrowing of the precession frequency linewidth.
Assuming that the local (effective nhf) field correlation
function is described by
| 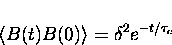 |
(14) |
(where 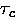 is the correlation time and
is the correlation time and 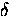 is the width of the field distribution) the relaxation
function is [56]
is the width of the field distribution) the relaxation
function is [56]
|  |
(15) |
In the case of sufficiently slow hopping when 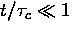 ,the TF relaxation function approaches the Gaussian form of the static limit
,the TF relaxation function approaches the Gaussian form of the static limit
independent of 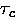 , with relaxation rate
, with relaxation rate 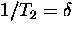 .In the case of fast hopping the effective nhf field is
averaged over many sites
resulting in the motional narrowing of the linewidth; the
relaxation function tends to an exponential form:
.In the case of fast hopping the effective nhf field is
averaged over many sites
resulting in the motional narrowing of the linewidth; the
relaxation function tends to an exponential form:
with the smaller relaxation rate
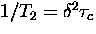 . In the limit of fast hopping
the TF and LF experiments should give the same relaxation rates.
Figure 6.20 shows examples of the relaxation function
for several correlation times corresponding to mean hop rates
from 0 to 50
. In the limit of fast hopping
the TF and LF experiments should give the same relaxation rates.
Figure 6.20 shows examples of the relaxation function
for several correlation times corresponding to mean hop rates
from 0 to 50 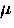 s-1.
s-1.
Figure 6.20:
Theoretical muonium spin relaxation functions
in transverse field, showing the change from Gaussian to exponential
form and reduction in the relaxation rate due to motional narrowing.
For all curves 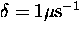 .
.
 |
Figure 6.21 shows the muonium spin relaxation
rates measured in s-N2by TF and LF 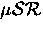 experiments.
The qualitative temperature dependence of the relaxation
rates and the hop rate is entirely consistent with the following
interpretation.
At low temperatures (T < 5K) muonium is nearly static; the TF
experiment measured a T-independent relaxation rate
as expected in the slow-hopping limit.
Between about 9 K and 20 K the TF relaxation rate drops,
as expected if the muonium diffuses faster as temperature rises.
The LF relaxation rates in 4, 8 and 12 G reach their
maxima, where
experiments.
The qualitative temperature dependence of the relaxation
rates and the hop rate is entirely consistent with the following
interpretation.
At low temperatures (T < 5K) muonium is nearly static; the TF
experiment measured a T-independent relaxation rate
as expected in the slow-hopping limit.
Between about 9 K and 20 K the TF relaxation rate drops,
as expected if the muonium diffuses faster as temperature rises.
The LF relaxation rates in 4, 8 and 12 G reach their
maxima, where
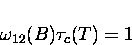
is satisfied,
at progressively higher temperatures.
Between about 11 K and 15 K the relaxation rate in LF becomes
field-independent and approaches the TF relaxation rate,
also indicating that the hop rate increases with temperature
in this part of the data.
Making use of Eqs. (6.13),(6.18)
and (6.19)
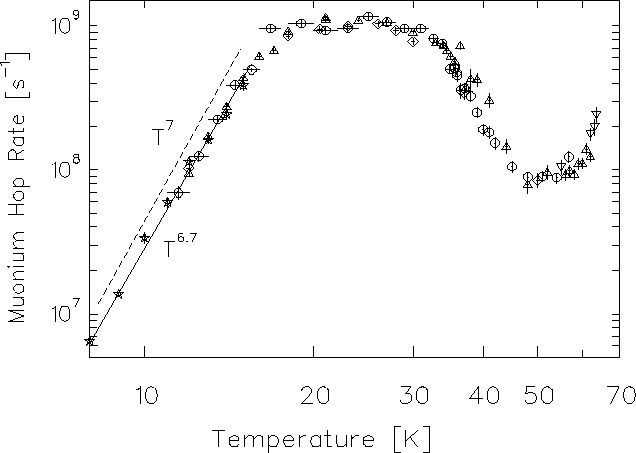
we can extract the muonium hop rate 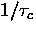 as a function of temperature,
as shown in Fig. 6.22.
The LF experiments measured a diffusion rate
increasing as T6.7(1) up to 15 K.
The TF data extend this to higher temperatures where
the correlation time
as a function of temperature,
as shown in Fig. 6.22.
The LF experiments measured a diffusion rate
increasing as T6.7(1) up to 15 K.
The TF data extend this to higher temperatures where
the correlation time 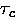 is so short that the
LF relaxation rate becomes nearly independent of
magnetic field and approaches the TF relaxation rate.
Between about 20 and 30 K the hop rate reaches its maximum;
the TF relaxation rate become T-independent
at about 0.4
is so short that the
LF relaxation rate becomes nearly independent of
magnetic field and approaches the TF relaxation rate.
Between about 20 and 30 K the hop rate reaches its maximum;
the TF relaxation rate become T-independent
at about 0.4 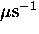 .If the hop rate here is limited only by the coherent
tunnelling bandwidth, we can estimate
.If the hop rate here is limited only by the coherent
tunnelling bandwidth, we can estimate
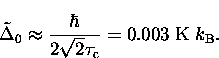
It is also possible that the relaxation rate due to the
motionally averaged nuclear hyperfine interaction with N2moments
is even smaller, but is overwhelmed by
spin relaxation due to other causes, such as the muonium
atoms diffusing to chemically active impurities or impurites
with electronic moments such as O2 that
immediately depolarize any muonium atom that strays near.
Above about 50 K the TF relaxation rate increases
as the hop rate drops with increasing temperature,
a key characteristic of incoherent (2-phonon) quantum diffusion,
although theory predicts a much weaker temperature dependence
at such a large fraction of the Debye temperature.
Figure 6.21:
Muonium spin polarization relaxation rates measured
in solid nitrogen. Stars (12G), boxes (8G) and crosses (4G)
indicate the LF data and all other points are in
TF  5G for different samples.
5G for different samples.
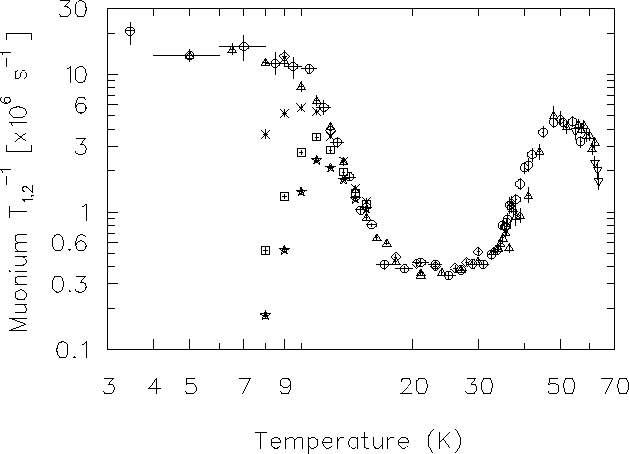 |
Figure 6.22:
Muonium hop rate 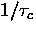 in solid N2 obtained from the
spin relaxation rates 1/T1 and 1/T2 measured in LF and TF
respectively. Stars indicate the results from LF data; all other
points are from TF data. The power-law fit is shown by the solid
line; the nearly parallel T7 theoretical dependence is shown by the
dashed line, offset for clarity.
in solid N2 obtained from the
spin relaxation rates 1/T1 and 1/T2 measured in LF and TF
respectively. Stars indicate the results from LF data; all other
points are from TF data. The power-law fit is shown by the solid
line; the nearly parallel T7 theoretical dependence is shown by the
dashed line, offset for clarity.
 |



Next: 6.4 Numerical Calculations: Solid
Up: 6 Quantum Diffusion II:
Previous: 6.2 Muonium Diffusion in


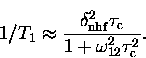
![]() and
and ![]() are very nearly equal
(see Appendix A for definitions of these and the other
muonium frequencies
are very nearly equal
(see Appendix A for definitions of these and the other
muonium frequencies ![]() and
and ![]() )the splitting between these two lines is
)the splitting between these two lines is


![]() experiments.
The qualitative temperature dependence of the relaxation
rates and the hop rate is entirely consistent with the following
interpretation.
At low temperatures (T < 5K) muonium is nearly static; the TF
experiment measured a T-independent relaxation rate
as expected in the slow-hopping limit.
Between about 9 K and 20 K the TF relaxation rate drops,
as expected if the muonium diffuses faster as temperature rises.
The LF relaxation rates in 4, 8 and 12 G reach their
maxima, where
experiments.
The qualitative temperature dependence of the relaxation
rates and the hop rate is entirely consistent with the following
interpretation.
At low temperatures (T < 5K) muonium is nearly static; the TF
experiment measured a T-independent relaxation rate
as expected in the slow-hopping limit.
Between about 9 K and 20 K the TF relaxation rate drops,
as expected if the muonium diffuses faster as temperature rises.
The LF relaxation rates in 4, 8 and 12 G reach their
maxima, where
![]()
![]() as a function of temperature,
as shown in Fig. 6.22.
The LF experiments measured a diffusion rate
increasing as T6.7(1) up to 15 K.
The TF data extend this to higher temperatures where
the correlation time
as a function of temperature,
as shown in Fig. 6.22.
The LF experiments measured a diffusion rate
increasing as T6.7(1) up to 15 K.
The TF data extend this to higher temperatures where
the correlation time ![]() is so short that the
LF relaxation rate becomes nearly independent of
magnetic field and approaches the TF relaxation rate.
Between about 20 and 30 K the hop rate reaches its maximum;
the TF relaxation rate become T-independent
at about 0.4
is so short that the
LF relaxation rate becomes nearly independent of
magnetic field and approaches the TF relaxation rate.
Between about 20 and 30 K the hop rate reaches its maximum;
the TF relaxation rate become T-independent
at about 0.4 ![]() .If the hop rate here is limited only by the coherent
tunnelling bandwidth, we can estimate
.If the hop rate here is limited only by the coherent
tunnelling bandwidth, we can estimate