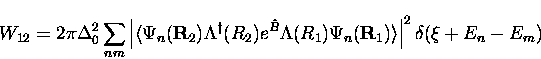
A second effect, called by Kagan and Klinger fluctuational preparation of the barrier (FPB), will always tend to increase the tunnelling rate. Thermal motion of the atoms that define the potential barrier between two sites will sometimes raise and other times lower the height of the barrier. The total tunnelling rate will be determined largely by the rate during the time when the atoms take on configurations most conducive to the transition; the path of least resistance contributes the most. Both of these effects depend on the thermal fluctuations of atomic positions, and so are expected to have a larger influence as temperature rises. Barrier fluctuations will have their greatest effect at high temperatures since long-wavelength phonons simply shift whole regions of the lattice without changing the relative positions of atoms close to the interstitial. Short wavelength phonons will produce shifts in the separation of adjacent atoms, the ones that define the shape of the barrier, and are excited at temperatures approaching the Debye temperature. The transition rate including the effects of both polaron deformation and barrier fluctuations is
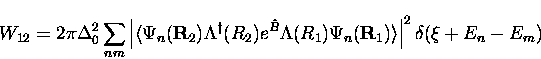 |
(13) |
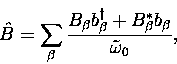 |
(14) |
Expanding the square of the matrix element in Eq. (5.22)
and writing the ![]() -function
in terms of its Fourier transform, we can write the hop rate
as an integral over time
-function
in terms of its Fourier transform, we can write the hop rate
as an integral over time
Expanding each part in terms of the creation and annihilation
operators ![]() ,
, ![]() ,(for which we have the commutator
,(for which we have the commutator ![]() ,
, ![]() since phonons are bosons)
since phonons are bosons)
![\begin{displaymath}
B_0= \sum_{\beta} - \frac{B_{-\beta} [C_{\beta}(R_1) + C_{\beta}(R_2) ] }
{\omega_{\beta} \tilde \omega_0}.\end{displaymath}](img147.gif) |
(15) |
Doing the same calculation with the second set of time-dependent operators,
[with ![]() ]and then calculating the expectation value of the product of all
six operators gives the result
]and then calculating the expectation value of the product of all
six operators gives the result
 |
(16) |
Introducing two more sums over the phonon spectrum
![\begin{displaymath}
\Omega_{{\rm 1ph}}(\omega) = \pi T \sum_{\beta} \frac{1}{\om...
...vert B_{\beta}\vert^2 \right]
\, \delta(\omega_{\beta}- \omega)\end{displaymath}](img150.gif) |
(17) |
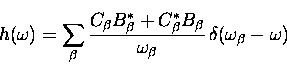 |
(18) |
results, with more algebra, in the general expression
Due to the presence of the oscillating terms, e-F1(t) is peaked
about t=0, and so makes the largest contribution to the integral
in Eq. (5.25)
near ![]() .
For small
.
For small ![]() and
and ![]() several
approximations can be
made to further simplify these expressions, leading to an expression that
yields its (approximate) temperature dependence in a more intuitive way.
several
approximations can be
made to further simplify these expressions, leading to an expression that
yields its (approximate) temperature dependence in a more intuitive way.
Using these approximations and defining the following functions enables us to write an expression for the hop rate in which all the sums over the phonon population have been integrated out.
In terms of these functions we obtain
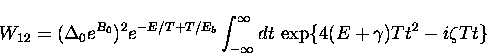 |
(19) |
This integral can be solved exactly, giving a simple expression for the hop rate
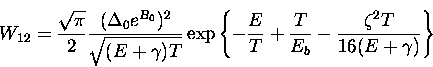 |
(20) |
If the coupling to barrier fluctuations turns out to be negligible
(that is, letting all the ![]() 's go to zero) then we recover
the familiar expression
's go to zero) then we recover
the familiar expression
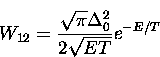 |
(21) |
The motivation for making all of these approximations
was to allow one to write a simple expression for
the hop rate. It turns out that the existence of an
upper cut-off frequency (essentially the Debye frequency
![]() ) in the sums over the phonon
modes makes it possible to calculate the integrals
in the general form, Eq. (5.35), by numerical
methods without making any further approximations.
This approach is taken in the analysis of Mu diffusion
in solid Xe.
) in the sums over the phonon
modes makes it possible to calculate the integrals
in the general form, Eq. (5.35), by numerical
methods without making any further approximations.
This approach is taken in the analysis of Mu diffusion
in solid Xe.