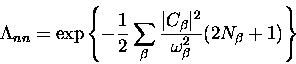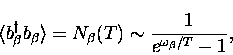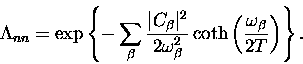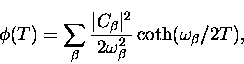


Next: 5.4 Barrier Fluctuations
Up: 5 Quantum Diffusion I:
Previous: 5.2 Renormalization of the
In the case of a particle-phonon coupling linear in
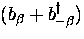 we write the Hamiltonian of the excitations of the lattice
plus the interaction between the lattice atoms and
the interstitial muonium (which, in the adiabatic approximation
is at the centre of the well, so this Hamiltonian depends on
displacements of the lattice atoms only)
we write the Hamiltonian of the excitations of the lattice
plus the interaction between the lattice atoms and
the interstitial muonium (which, in the adiabatic approximation
is at the centre of the well, so this Hamiltonian depends on
displacements of the lattice atoms only)
where the sum is over all phonons present.
The coupling constant 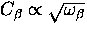 governs the strength of the interaction with the interstitial.
[54,53]
governs the strength of the interaction with the interstitial.
[54,53]
The effect of the polaron deformation and the origin of the
associated trapping potential become apparent in
calculating 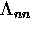 .We start by using a normal oscillator shift
.We start by using a normal oscillator shift 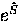 in which
in which
| 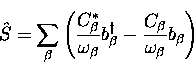 |
(5) |
to define
new operators 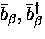 ,
,
Substituting these operators into the Hamiltonian,
Eq. (5.9) becomes
(noting that 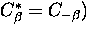
| 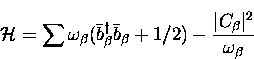 |
(6) |
which simply corresponds to a new set of harmonic oscillators
with a shift in energy, but the one-phonon interaction has now
been eliminated.
The wave functions we need to construct are then
We are now able to write the matrix elements of 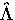
| 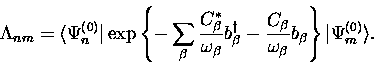 |
(7) |
The polaron effect corresponds to the diagonal elements 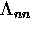 ,
,
| 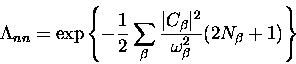 |
(8) |
which, with the number of phonons of frequency 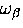 now a function of temperature
now a function of temperature
| 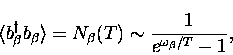 |
(9) |
reduces to
(suppressing an overall constant)
| 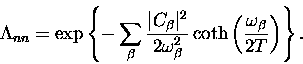 |
(10) |
It is usual in the literature to define the ``polaron exponent"
as the sum
| 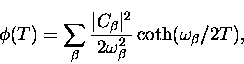 |
(11) |
so that
the polaron effect manifests itself as a renormalization
(reduction) of the raw tunnelling bandwidth 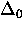
| 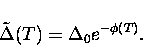 |
(12) |



Next: 5.4 Barrier Fluctuations
Up: 5 Quantum Diffusion I:
Previous: 5.2 Renormalization of the
![]() we write the Hamiltonian of the excitations of the lattice
plus the interaction between the lattice atoms and
the interstitial muonium (which, in the adiabatic approximation
is at the centre of the well, so this Hamiltonian depends on
displacements of the lattice atoms only)
we write the Hamiltonian of the excitations of the lattice
plus the interaction between the lattice atoms and
the interstitial muonium (which, in the adiabatic approximation
is at the centre of the well, so this Hamiltonian depends on
displacements of the lattice atoms only)
![]() .We start by using a normal oscillator shift
.We start by using a normal oscillator shift ![]() in which
in which
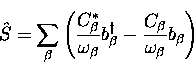
![]()
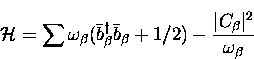
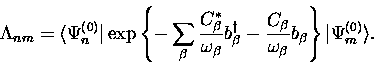
![]() ,
,