We would like to be able to write the wave functions of the
lattice with the particle present, ![]() ,in terms of the normal modes of the lattice
without an interstitial.
However,
,in terms of the normal modes of the lattice
without an interstitial.
However, ![]() is an eigenfunction of the Hamiltonian
which includes the lattice-interstitial interaction,
is an eigenfunction of the Hamiltonian
which includes the lattice-interstitial interaction,
By performing a transformation of the one-phonon interaction we can write these wave functions in the same basis, allowing us to evaluate the overlap,
![]()
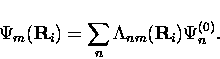 |
(1) |
Overall, the method of calculating the interstitial diffusion rate will be to describe the shifted atomic positions in both the initial and final states in terms of linear combinations of non-interacting environmental states, which include temperature-dependent numbers of phonons. The overlap between initial and final states is then given by the coefficients in these sums. Most of the following derivation will be the evaluation of the temperature dependence of these coefficients.
Fermi's Golden Rule then gives the transition rate
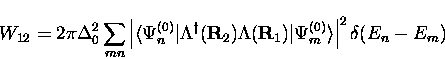 |
(2) |
We will consider two cases of coupling to lattice excitations - corresponding to the linear and quadratic terms of a Taylor expansion of the Hamiltonian - which govern the behavior at high and low temperatures respectively. In this theory, displacements of atoms from their equilibrium positions in a harmonic potential are being written in terms of the normal modes of the lattice.
Let us first consider a very simple example to introduce the
idea of writing oscillator displacement in terms of
operators.
In general, the Hamiltonian of a harmonic oscillator is the sum of
kinetic and potential energies
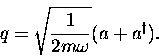 |
(3) |
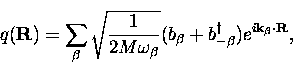 |
(4) |