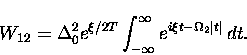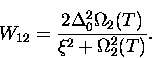


Next: 6 Quantum Diffusion II:
Up: 5 Quantum Diffusion I:
Previous: 5.4 Barrier Fluctuations
The second case we consider has the coupling to lattice
excitations taking a form quadratic in atomic displacements so
we now write the Hamiltonian, in terms of the same
shifted-mode phonon operators as before, as
| 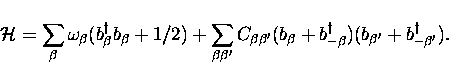 |
(22) |
We continue in the same framework we used in solving the
one-phonon problem. Again, we are interested in finding out how much
the initial and final states overlap, so we want to construct these
states in terms of unitary tranformations of the environmental states.
Now the full polaron operator in Eq. (5.24) becomes,
with an additional unitary operator for the two-phonon interaction,
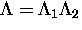 .Again, we write the transition rate, making use of the Fourier
transform of the
.Again, we write the transition rate, making use of the Fourier
transform of the 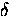 -function,
-function,
| 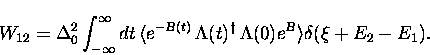 |
(23) |
Here 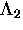 is composed of two parts that arise from the cross
terms in the product
is composed of two parts that arise from the cross
terms in the product
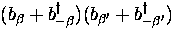 .
.
There are two kinds (not counting complex conjugates)
of two-phonon terms in this; those of the form
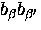 that create (or annihilate)
two separate phonons, and those of the form
that create (or annihilate)
two separate phonons, and those of the form
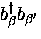 that
annihilate one phonon and create another, therefore allowing
scattering of one phonon from one state to another.
The largest contribution to the transition rate comes from
those terms where the shift of the phonon frequency due to scattering
is small;
that
annihilate one phonon and create another, therefore allowing
scattering of one phonon from one state to another.
The largest contribution to the transition rate comes from
those terms where the shift of the phonon frequency due to scattering
is small; 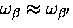 .For this reason the scattering part of the two-phonon
interaction is said to preserve the phonon population, but strictly
speaking it is not precisely unchanged. We are in a regime
where coherent (band) diffusion is partially ruined by
the scattering of phonons.
Further, in the limit of a small shift in phonon frequencies
so that
.For this reason the scattering part of the two-phonon
interaction is said to preserve the phonon population, but strictly
speaking it is not precisely unchanged. We are in a regime
where coherent (band) diffusion is partially ruined by
the scattering of phonons.
Further, in the limit of a small shift in phonon frequencies
so that 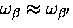 ,we have approximately
,we have approximately
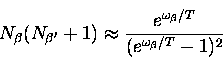
and we shall see the usual phonon density of states enters as
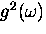 , not as a density of two-phonon states.
Keeping only the scattering terms from Eq. (5.43)
, not as a density of two-phonon states.
Keeping only the scattering terms from Eq. (5.43)
| 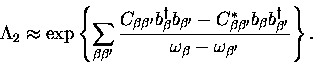 |
(24) |
We write out the matrix element by the same method as we
used for the one-phonon interaction and consider now each mode as
separable,
We see that renormalization of the tunnelling bandwidth 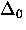 by the 1-phonon interaction still holds, but now we are also
including what will turn out to be a reduction of the effective
bandwidth due to the contribution of the two-phonon interaction,
corresponding to the terms of the form
by the 1-phonon interaction still holds, but now we are also
including what will turn out to be a reduction of the effective
bandwidth due to the contribution of the two-phonon interaction,
corresponding to the terms of the form
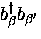 in
in
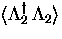 .
.
By the same method as we used earlier, we write out the
expectation value in terms of the boson operators
For small frequency shifts 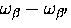 this is, to very good approximation,
this is, to very good approximation,
| 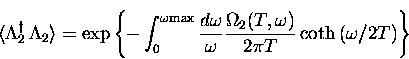 |
(25) |
with
| 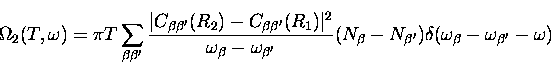 |
(26) |
We have put 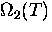 in this form so we can write
in this form so we can write
in which we have dropped the time-independent term,
since it is small for temperatures low compared
to typical 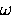 , and the frequency dependence of
, and the frequency dependence of
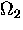 since we are in the limit of small differences
between phonon frequencies.
since we are in the limit of small differences
between phonon frequencies.
The hop rate is then
| 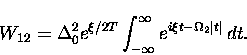 |
(27) |
What is the function 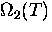 ?
Here it is clear that
?
Here it is clear that 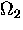 (which is always
a positive, real quantity) takes on the role of
an exponential relaxation (or damping) rate of the
transition amplitude.
The initial and final states during the
tunnelling transition have almost exactly the same energy, but phase
coherence is lost in the process of scattering phonons.
Coherence is suppressed when the transition time
(which is always
a positive, real quantity) takes on the role of
an exponential relaxation (or damping) rate of the
transition amplitude.
The initial and final states during the
tunnelling transition have almost exactly the same energy, but phase
coherence is lost in the process of scattering phonons.
Coherence is suppressed when the transition time  is relatively
long so that
is relatively
long so that 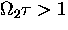 .The integral in Eq. (5.51) converges to
.The integral in Eq. (5.51) converges to
| 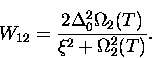 |
(28) |
The temperature dependence of the hop rate is then
determined by the de-coherence rate 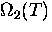 and
the interplay with the typical site-to-site energy shift
and
the interplay with the typical site-to-site energy shift 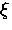 .
In the following section we will show that
.
In the following section we will show that 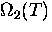 is
a strongly increasing function of temperature and also explore
the influence of the phonon density of states on the
diffusion rate.
is
a strongly increasing function of temperature and also explore
the influence of the phonon density of states on the
diffusion rate.



Next: 6 Quantum Diffusion II:
Up: 5 Quantum Diffusion I:
Previous: 5.4 Barrier Fluctuations
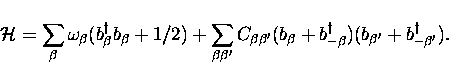
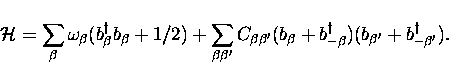
![]() .Again, we write the transition rate, making use of the Fourier
transform of the
.Again, we write the transition rate, making use of the Fourier
transform of the ![]() -function,
-function,
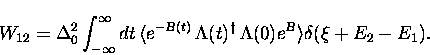
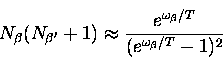
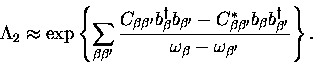
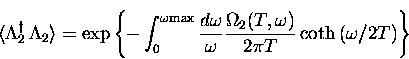
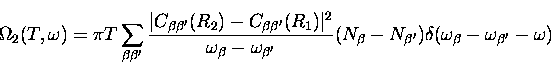
![]() in this form so we can write
in this form so we can write