Doping dependence of the size of moment

In the discussion above, the absence of muon spin precession in the Zn doped system was attributed to the macroscopic sample inhomogeneity. This discussion, at the same time, expects a muon spin relaxation in the Zn doped system with its rate mostly determined by the average relaxation rate $\bar{\Delta}$. Contrary to the precession, this relaxation rate is robust to the sample inhomogeneity, as shown in Fig.61. 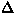Since in the Si-doped crystal the relaxation rate $\Delta$ was found to be proportional to the size of moments (Fig.60), the relaxation rates measured in the Zn-doped samples should also reflect the average size of the ordered moments.

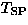As shown in the inset of Fig.57, the saturated relaxation rate [$\Delta(T\!\rightarrow\!0)$] takes a maximum at the optimum doping concentration. The increase of $\Delta(T\!\rightarrow\!0)$ in the Zn `under-doped' regime indicates a creation of static moments upon doping, being consistent with the suppression of $T_{\rm SP}$ and the enhancement of 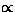$T_{\rm N}$ (Fig.53). The decrease of $\Delta(T\!\rightarrow\!0)$ in the Zn `over-doped' regime is partly attributed to trivial dilution of moments due to the Zn substitutions; even if the size of ordered moments doesn't change upon Zn doping, the muon relaxation rate should decrease as $\Delta(x)\sim\Delta_0(1-x)$,simply because of the decrease in the number of spins. Still, the experimental result suggests more pronounced decrease; the relaxation rate decreased by $\sim 20$ % [$\Delta(T\!\rightarrow\!0)\sim 5\rightarrow 4\, \mu{\rm s}^{-1}$] in the change of Zn concentration $x=4\rightarrow 8$ %. This result suggests that the ordered moments shrinks in the Zn over-doped regime.