



Next: Discussion
Up: 6.2 Spin-Peierls material CuGeO
Previous: Zn-doped systems
Recent technical development at TRIUMF made it possible to measure
small specimens, such as 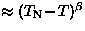 single crystal. We measured
such single crystals of Cu(Ge1-ySiy)O3 (y=2 %), using the newly developed
`low background apparatus', which has an additional particle counter
(veto-counter) on the beam path, behind the sample. If a muon misses the sample
and hits the veto-counter, it makes a rejection signal so that this
event is thrown away. This way, background-free measurements of
small crystals has become possible.
single crystal. We measured
such single crystals of Cu(Ge1-ySiy)O3 (y=2 %), using the newly developed
`low background apparatus', which has an additional particle counter
(veto-counter) on the beam path, behind the sample. If a muon misses the sample
and hits the veto-counter, it makes a rejection signal so that this
event is thrown away. This way, background-free measurements of
small crystals has become possible.
A single crystal of Si-doped system Cu(Ge1-ySiy)O3 (y=2 %) was synthesized
at Laboratoire de Chimie des Solides, Université Paris-Sud (Orsay, France),
using the floating zone method. A single
crystalline rod (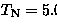 mm; long-axis = c-axis)
was cleaved to a thickness of
mm; long-axis = c-axis)
was cleaved to a thickness of 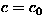 mm and tiled,
so that the surface area across the muon beam becomes large. We used three
such sliced pieces for our measurements.
mm and tiled,
so that the surface area across the muon beam becomes large. We used three
such sliced pieces for our measurements.
Figure 59:
(a) Zero-field  SR spectra of the Si 2% doped crystal, and (b) the
same spectra with longer time range. The solid lines are the fit with
the function described in the text (eq.59). The line drawn
on the 5.5 K data is a fit with Gaussian Kubo-Toyabe function from
nuclear dipolar fields.
SR spectra of the Si 2% doped crystal, and (b) the
same spectra with longer time range. The solid lines are the fit with
the function described in the text (eq.59). The line drawn
on the 5.5 K data is a fit with Gaussian Kubo-Toyabe function from
nuclear dipolar fields.
 |
In Fig.59,  SR spectra of the Si 2% doped system
are shown. A spontaneous muon spin precession was observed, indicating the
Néel order of the moments. We analyzed the spectra with the functional form:
SR spectra of the Si 2% doped system
are shown. A spontaneous muon spin precession was observed, indicating the
Néel order of the moments. We analyzed the spectra with the functional form:
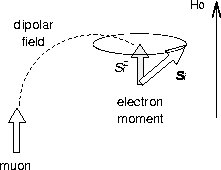
The first term of eq.59 corresponds to the `1/3-component'
in polycrystalline measurements; in a single crystal, the direction of
the local field depends on the crystal orientation (see
Fig.15 in Chapter 3), so that the muon spin
component which does not show a precession could be any amplitude
( defined in Fig.15 of Chapter 3).
The time-dependent part of the muon spin polarization
seems to have two sub-components; one precession signal (the second
term of eq.59) and relaxation (the third term).
defined in Fig.15 of Chapter 3).
The time-dependent part of the muon spin polarization
seems to have two sub-components; one precession signal (the second
term of eq.59) and relaxation (the third term).
In Fig.60, we show the precession
frequency (f) and the relaxation rate (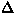 ) as a function of
temperature. It was found that relaxation rate (
) as a function of
temperature. It was found that relaxation rate (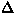 ) scales with
the precession frequency (f), as shown in the inset of
Fig.60. Since the frequency (f) is
proportional to the size of the ordered moments, this scaling result
indicates that the relaxation (the third term of eq.59) is
caused by a distributed local field which reflects the moment size.
) scales with
the precession frequency (f), as shown in the inset of
Fig.60. Since the frequency (f) is
proportional to the size of the ordered moments, this scaling result
indicates that the relaxation (the third term of eq.59) is
caused by a distributed local field which reflects the moment size.
A power-law fit (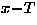 ) to the frequency (f)
and the relaxation rate (
) to the frequency (f)
and the relaxation rate (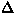 ) found
) found 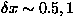 K and
K and 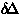 .The exponent (
.The exponent (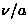 ) is consistent with that of the antiferromagnetic
Bragg peak intensity observed in (Cu1-xZnx)GeO3 [161].
) is consistent with that of the antiferromagnetic
Bragg peak intensity observed in (Cu1-xZnx)GeO3 [161].
Figure 60:
Temperature dependence of the precession frequency (f) and the
relaxation rate (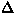 ). The dashed line is a power-law fit
described in the text. The inset is the ratio
). The dashed line is a power-law fit
described in the text. The inset is the ratio  , which was
found to be temperature independent.
, which was
found to be temperature independent.
 |




Next: Discussion
Up: 6.2 Spin-Peierls material CuGeO
Previous: Zn-doped systems
![]() mm; long-axis = c-axis)
was cleaved to a thickness of
mm; long-axis = c-axis)
was cleaved to a thickness of ![]() mm and tiled,
so that the surface area across the muon beam becomes large. We used three
such sliced pieces for our measurements.
mm and tiled,
so that the surface area across the muon beam becomes large. We used three
such sliced pieces for our measurements.

 defined in Fig.15 of Chapter 3).
The time-dependent part of the muon spin polarization
seems to have two sub-components; one precession signal (the second
term of eq.59) and relaxation (the third term).
defined in Fig.15 of Chapter 3).
The time-dependent part of the muon spin polarization
seems to have two sub-components; one precession signal (the second
term of eq.59) and relaxation (the third term).
![]() ) as a function of
temperature. It was found that relaxation rate (
) as a function of
temperature. It was found that relaxation rate (![]() ) scales with
the precession frequency (f), as shown in the inset of
Fig.60. Since the frequency (f) is
proportional to the size of the ordered moments, this scaling result
indicates that the relaxation (the third term of eq.59) is
caused by a distributed local field which reflects the moment size.
) scales with
the precession frequency (f), as shown in the inset of
Fig.60. Since the frequency (f) is
proportional to the size of the ordered moments, this scaling result
indicates that the relaxation (the third term of eq.59) is
caused by a distributed local field which reflects the moment size.
![]() ) to the frequency (f)
and the relaxation rate (
) to the frequency (f)
and the relaxation rate (![]() ) found
) found ![]() K and
K and ![]() .The exponent (
.The exponent (![]() ) is consistent with that of the antiferromagnetic
Bragg peak intensity observed in (Cu1-xZnx)GeO3 [161].
) is consistent with that of the antiferromagnetic
Bragg peak intensity observed in (Cu1-xZnx)GeO3 [161].
