Haldane systems

The two systems introduced above have a geometrical reason for two specific spins to form a singlet pair. In the next system, the S=1 antiferromagnetic spin chain, the value of the spin (integer) makes it possible to form singlet pairs.

In 1983, F. D. M. Haldane conjectured that in the Heisenberg model, antiferromagnetic chains of integer spins would show a finite energy gap between the singlet ground state and the triplet first excited state. He also claimed that the spin correlation of the ground state quickly decays as an exponential function of distance [22,23]. These two features propose that the integer-spin Heisenberg model has a highly disordered ground state, which is far from the Néel state. Haldane's predictions were surprising, because the same Heisenberg model, with S=1/2 spins, is gap-less and has a power-law decay of the correlation function [11].

In 1987, an intuitive picture for the Haldane's ground state was proposed, with an exactly soluble S=1 spin Hamiltonian [24,25]:

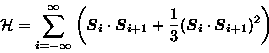$${\cal H}=\sum_{i=-\infty}^{\infty}\left ({\mbox{\boldmath$S$... ...ath}_i}\cdot{\mbox{\boldmath$S$\unboldmath}_{i+1}})^{2}\right )$$ (1)

which adds a biquadratic term to the Heisenberg model. The ground state of this Hamiltonian (Valence Bond Solid state: Fig.5b) was mathematically proved to have a spin-gap and an exponentially decaying correlation function [24,25,26,27]. The model without the biquadratic term (Heisenberg model) is believed to have a similar ground state structure to that of the Valence Bond Solid state. See Chapter 5 for more about the Haldane systems.

  

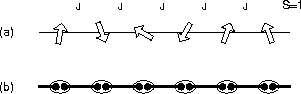
Figure 5: (a) An S=1 spin chain. (b) A schematic view of the Valence Bond Solid (VBS) state, which is based on many singlet pairs. The circle at each site represents the projection of two S=1/2 spins to one S=1.