5.1.2 The Valence-Bond-Solid Hamiltonian

In 1987, I. Affleck, T. Kennedy, E. H. Lieb and H. Tasaki proposed a Hamiltonian for S=1 spins [24]:

which is the antiferromagnetic Heisenberg model modified by a biquadratic second term. The authors of Ref. [24,25] rigorously obtained the ground state, which has an exponentially-decaying correlation function and a finite energy gap to the excited states. The exact ground state, which is known as `Valence Bond Solid state', is constructed as follows:

(1)

decompose the S=1 spins at each site into two S=1/2 spins (Fig.35a)

(2)

make singlet bonds between adjacent S=1/2 spins (Fig.35b)

(3)

symmetrize the two S=1/2's on each site to restore the S=1 degrees of freedom (Fig.35c).

The VBS ground state is non-magnetic singlet in nature, as it is built from many singlet pairs. From numerical calculations of the VBS Hamiltonian (eq.41) with arbitrary magnitudes of the biquadratic term (1/3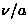$\rightarrow$$\beta$), it has been shown that the non-magnetic ground state of the pure Heisenberg model ($\beta=0$) belongs to the same category as the VBS ground state [63,64].

Another characteristic of the VBS state appears when a spin site is substituted with a foreign ion (Fig.35d). The foreign ion breaks two singlet pairs, and introduces two S=1/2 paramagnetic spins. The S=1/2 degrees of freedom have actually been observed in electron spin resonance (ESR) measurements of a Haldane material NENP (see section 5.1.4).

  

Figure 35: (a) S=1 antiferromagnetic spin chain. Each S=1 spin is decomposed into two S=1/2 spins. (b) Singlet pairing of the adjacent S=1/2 spins. (c) The Valence Bond Solid (VBS) state. The two S=1/2 spins on each lattice point are symmetrized to restore S=1. (d) The VBS state doped with a foreign ion.