



Next: 2.2.4 Counter/muon spin geometries
Up: 2.2 Experimental setup for
Previous: Cryostats
The signals from the muon/positron counters are shaped to a logical
pulse using the CFD (Constant Fraction Discriminator),
which is commonly used in nuclear experiments. The logical pulses
are handled by the circuits shown in Fig.12, in order
to take the time spectrum of the  decay. The main scheme of the
electronics follows the thick solid lines; the `muon signal' starts
the stopwatch called TDC (Time to Digital Converter) and one of the
`positron signals' stops it. The elapsed time between these two events
is stored in the histogram memory, along with the information of which
positron counter gave the stop signal. The histogram memory is read by
the data-taking VAX-computer typically every 5 minutes.
decay. The main scheme of the
electronics follows the thick solid lines; the `muon signal' starts
the stopwatch called TDC (Time to Digital Converter) and one of the
`positron signals' stops it. The elapsed time between these two events
is stored in the histogram memory, along with the information of which
positron counter gave the stop signal. The histogram memory is read by
the data-taking VAX-computer typically every 5 minutes.
Figure 12:
A block diagram of the logical circuit for a  SR measurement.
SR measurement.
 |
The circuit is equipped with `pile-up rejection'
logic (thin solid line in Fig.12), which is necessary for
 SR measurements using a continuous beam, as at TRIUMF. This circuit rejects
situations where more than two muons reside in the apparatus within the
experimental time window; in this situation, there is no way of knowing
which muon decays to a given positron, and therefore, the data must be
thrown away. The gate generator with the dashed lines
determines the time range of interest for the measurements
(
SR measurements using a continuous beam, as at TRIUMF. This circuit rejects
situations where more than two muons reside in the apparatus within the
experimental time window; in this situation, there is no way of knowing
which muon decays to a given positron, and therefore, the data must be
thrown away. The gate generator with the dashed lines
determines the time range of interest for the measurements
(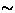 12
12  s). This time range is usually set
s). This time range is usually set 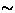 500 ns shorter
than the time window for the pileup rejection.
500 ns shorter
than the time window for the pileup rejection.
Figure 13:
A typical time spectrum of one positron counter. The inset
shows the same spectrum at the early time range.
 |
Using the electronics described as above, as well as the muon-beam and
the spectrometer, one obtains the time spectrum of the  decay, as shown in
Fig.13. There is, however, random background
overlapping the spectrum, an inevitable feature of continuous-beam
experiments. Usually, one assumes that the background is
time independent, and estimates its level from the spectrum at the
t<0 range (the inset of Fig.13). The estimated
background is evenly subtracted from the measured spectrum. The existence of the
background sets the technical upper-limit of the experimental time
range (
decay, as shown in
Fig.13. There is, however, random background
overlapping the spectrum, an inevitable feature of continuous-beam
experiments. Usually, one assumes that the background is
time independent, and estimates its level from the spectrum at the
t<0 range (the inset of Fig.13). The estimated
background is evenly subtracted from the measured spectrum. The existence of the
background sets the technical upper-limit of the experimental time
range (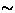 12
12  s) available for the continuous-beam
s) available for the continuous-beam  SR method.
SR method.
After subtracting the background, one calculates the corrected asymmetry
(eq.12), and obtains the time evolution of the muon spin
polarization, as shown in Fig.9b.




Next: 2.2.4 Counter/muon spin geometries
Up: 2.2 Experimental setup for
Previous: Cryostats

![]() SR measurements using a continuous beam, as at TRIUMF. This circuit rejects
situations where more than two muons reside in the apparatus within the
experimental time window; in this situation, there is no way of knowing
which muon decays to a given positron, and therefore, the data must be
thrown away. The gate generator with the dashed lines
determines the time range of interest for the measurements
(
SR measurements using a continuous beam, as at TRIUMF. This circuit rejects
situations where more than two muons reside in the apparatus within the
experimental time window; in this situation, there is no way of knowing
which muon decays to a given positron, and therefore, the data must be
thrown away. The gate generator with the dashed lines
determines the time range of interest for the measurements
(![]() 12
12 ![]() s). This time range is usually set
s). This time range is usually set ![]() 500 ns shorter
than the time window for the pileup rejection.
500 ns shorter
than the time window for the pileup rejection.
