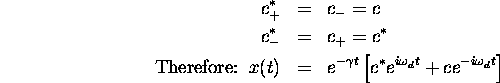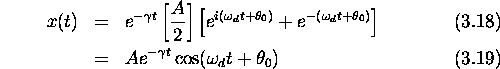Next: Experiment
Up: Damped Harmonic Motion
Previous: Damped Harmonic Motion
Consider a mass m on a spring with spring constant k, as shown in
Fig. 3.5. In addition to the spring force acting on the mass
(-kx), we will also assume that dissipative forces act on the mass.
These dissipative forces could be generated
within the spring itself, or due to the fluid through
which the mass moves. We will assume that the dissipative forces can be written
as 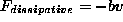 where v is the velocity of the mass.
where v is the velocity of the mass.

Figure: Mass on a spring
We can write F=ma for the mass:
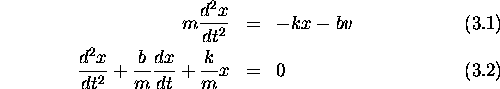
This is a second order differential equation whose general solution should have two
functions with two arbitrary constants.
We can solve by rewriting Eq. (3.2) as follows:
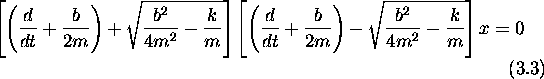
where the operator
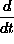 acts on all terms to the right of it.
The general solution of Eq. (3.3)
is the sum of solutions obtained from
setting the result of each of each first order operation on x
equal to zero.
acts on all terms to the right of it.
The general solution of Eq. (3.3)
is the sum of solutions obtained from
setting the result of each of each first order operation on x
equal to zero.
We can set
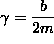 and
and
 giving:
giving:
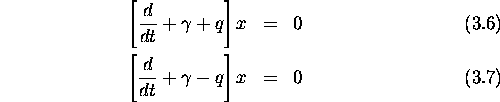
which gives for x(t):
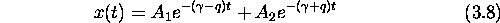
Clearly q can be complex (for example, take b=0, corresponding to the case
where there is no damping). We can distinguish three different regimes for different
possible values of q
- Overdamped (q real > 0)
Here x(t) is a decaying function of time
with two different decay time constants:
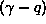 and
and
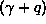 .
.
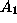 and
and
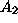 are determined by the intial
conditions (such as position and velocity).
For example, if the initial velocity
is zero, then
are determined by the intial
conditions (such as position and velocity).
For example, if the initial velocity
is zero, then
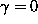 (you should check this) and
(you should check this) and
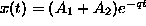 .
.
- Critically Damped (q real = 0)
Here q=0.
Since the two first order equations are the same, they only give one function
and constant. Since we need two independent functions and constants to satisfy
possible boundary conditions we return to the original equation with q=0.
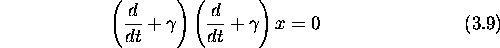
We substitute

giving
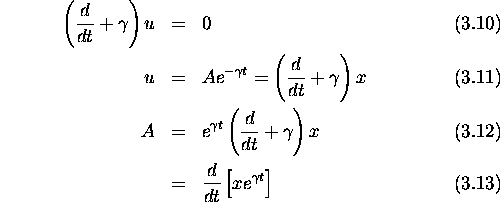
Integrating both sides with respect to time gives
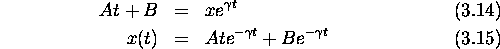
- Underdamped (q imaginary)
With q imaginary, we can write
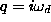 where
where
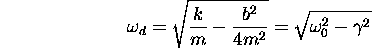
where
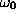 would be the oscillation frequency of the system in the
absence of damping.
would be the oscillation frequency of the system in the
absence of damping.
We can rewrite the general solution
[Eq. (3.8)]
for x(t):
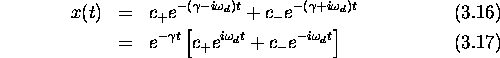
but x is real (after all it is the position of an object), therefore
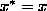 (x equals its complex conjugate). This gives:
(x equals its complex conjugate). This gives:
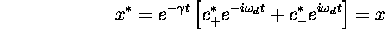
Therefore:
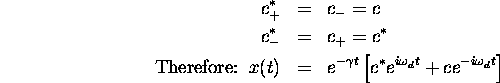
We can write

giving:
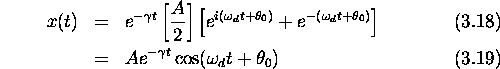



Next: Experiment
Up: Damped Harmonic Motion
Previous: Damped Harmonic Motion
![]() where v is the velocity of the mass.
where v is the velocity of the mass.
![]() and
and
 giving:
giving:
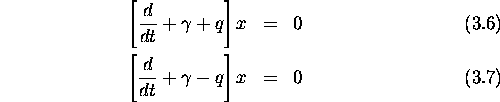
![]()
![]()
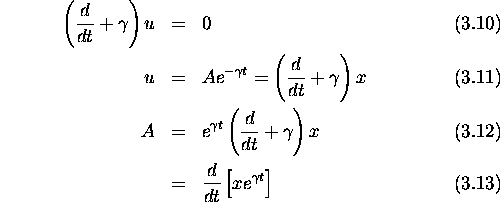
![]()
![]()
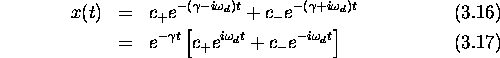
![]()