The direct evaluation of Eq. (6.20) by numerical
methods was performed to generate the theoretical function used in
fitting the temperature dependence of the Mu hop rate in terms
of three parameters; the tunnelling bandwidth ![]() ,
and dimensionless coupling parameters
,
and dimensionless coupling parameters ![]() and
and
![]() . Since the phonon spectrum includes an
arbitrary normalization that is folded into the coupling parameters,
the overall normalization is arbitrary. However, the ratio of the
coupling parameters tells us their relative strength, and
determines the course of the temperature dependence.
. Since the phonon spectrum includes an
arbitrary normalization that is folded into the coupling parameters,
the overall normalization is arbitrary. However, the ratio of the
coupling parameters tells us their relative strength, and
determines the course of the temperature dependence.
Figure 6.29(a) shows an example of the integrand of Eq. (6.20), a function of time. The point to be made here is that the high temperature expansion of the general theory is clearly not appropriate for all values of the coupling constants. The structure in this function away from t=0 is due to phonons in the middle of the phonon spectrum; the highest frequencies contribute most to the region near t=0.
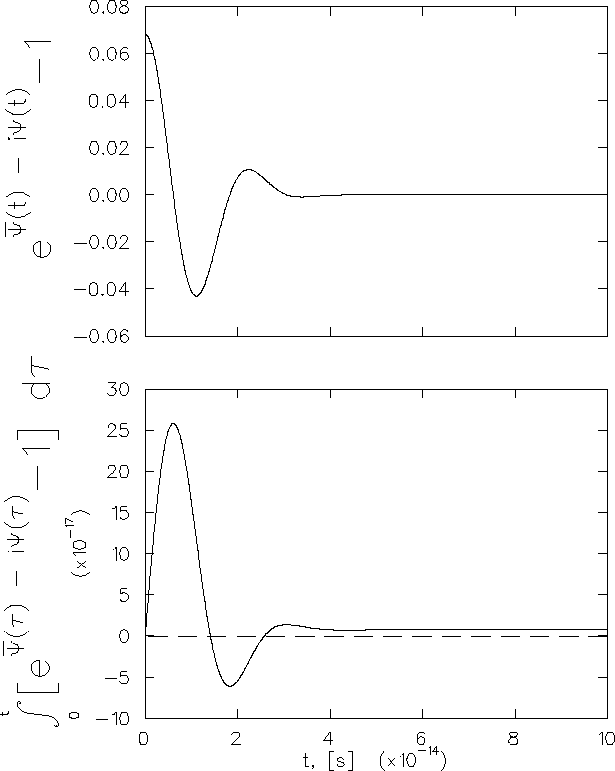 |
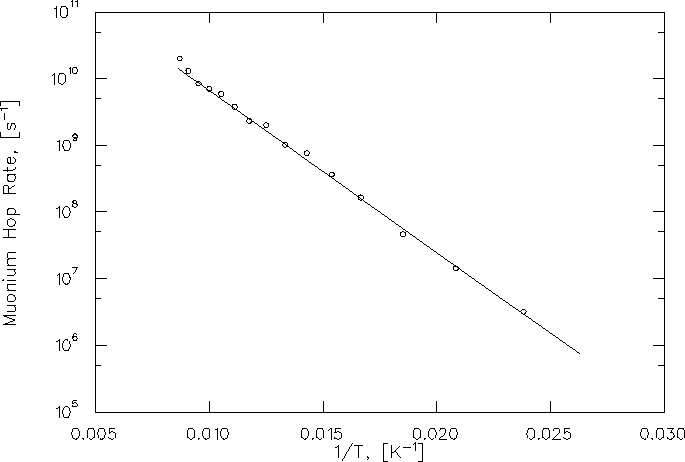 |
Numerical evaluation of the integrals is made
difficult due to the oscillatory nature of the integrand, which
contains terms in ![]() while
while ![]() ranges from zero to, in principle, infinity.
However, the existence of an upper cut-off in the phonon
spectrum at the Debye frequency allows one to carry
out the integration to a time t
such that an accurate estimate of the integral in the limit
that
ranges from zero to, in principle, infinity.
However, the existence of an upper cut-off in the phonon
spectrum at the Debye frequency allows one to carry
out the integration to a time t
such that an accurate estimate of the integral in the limit
that ![]() can be made.
(The program that performs this calculation is
discussed in Apppendix B, complete with the code.)
Fitting the data with hop rates calculated in this model
gives the parameter values
can be made.
(The program that performs this calculation is
discussed in Apppendix B, complete with the code.)
Fitting the data with hop rates calculated in this model
gives the parameter values
![]() and
and ![]() .The resulting curve is also shown by the solid line
in figure Fig. 6.30.
The values of the parameters imply that the suppression of tunnelling
due to the polaron self-trapping is overwhelmingly
large in comparison to the benefit gained from barrier height
fluctuations.
A fit with the model of Flynn and Stoneham, with the
hop rate given by Eq. (5.40)
in which
the barrier fluctuations do not enter, gives a similar
fit with parameter values
.The resulting curve is also shown by the solid line
in figure Fig. 6.30.
The values of the parameters imply that the suppression of tunnelling
due to the polaron self-trapping is overwhelmingly
large in comparison to the benefit gained from barrier height
fluctuations.
A fit with the model of Flynn and Stoneham, with the
hop rate given by Eq. (5.40)
in which
the barrier fluctuations do not enter, gives a similar
fit with parameter values ![]() = 2.50(5)
= 2.50(5) ![]() and
activation energy E = 0.0508(2) eV, also essentially indistinguishable
from the full one-phonon theory.
and
activation energy E = 0.0508(2) eV, also essentially indistinguishable
from the full one-phonon theory.