Understanding the most important ways phonons affect the tunnelling rate is the key problem in quantum diffusion of neutral interstitials. Short-wavelength phonons produce the greatest relative motion of adjacent atoms, so these should have the greatest influence in re-shaping the potential barrier between sites. We can therefore expect that the effect of barrier fluctuations on the tunnelling rate should be most apparent when these phonons are excited - at temperatures comparable to the Debye temperature.
The influence of the thermal motion
of lattice atoms on the diffusion rate via
barrier fluctuations
is probably best detected by measuring the hop rate
over as wide a range of temperatures as possible, so
that the onset of barrier fluctuations becomes apparent,
while tunnelling diffusion still dominates over
classical over-barrier diffusion.
A light interstitial can follow the fluctuations of the
lattice adiabatically, and also has a larger bandwidth
for tunnelling.
It follows that the most favourable conditions
for detecting the effect of thermal fluctuations on the
tunnelling rate would be with a light interstitial in a
lattice with a low Debye temperature.
In such cases the lattice can be hot enough for the entire
phonon spectum to be appreciably excited, but still
at temperatures where quantum effects should dominate
interstitial diffusion.
Muonium diffusion in solid Xe is an extreme example
of a light particle in a heavy, weakly interacting lattice,
(![]() )
and as such offers the best possibility to date of detecting
the effect of lattice dynamics on light interstitial quantum
diffusion.
)
and as such offers the best possibility to date of detecting
the effect of lattice dynamics on light interstitial quantum
diffusion.
Earlier we drived an expression, Eq. 5.35, for the hop rate at intermediate temperatures where the interstitial diffuses by phonon-mediated activated hopping. This can be rewritten in the form
![\begin{displaymath}
1/\tau_c=4 \Delta^2_0 e^{2(G-\phi)} \int_{-\infty}^{\infty} dt
\left [ e^{{\bar \Psi(t)} - i \Psi(t)} -1 \right ]\end{displaymath}](img257.gif) |
(16) |
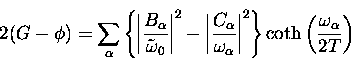 |
(17) |
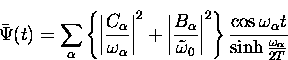 |
(18) |
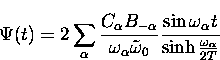 |
(19) |
The couplings are assumed to follow the long wavelength
asymptotic behavior, [53]
Replacing the sums over phonons by integrals over the phonon density of states this is approximately
![\begin{displaymath}
2(G-\phi) = \int d\omega \/g(\omega) \coth \left ( \frac{\om...
...{\omega}{\Theta_D} - \lambda_p \frac{\Theta_D}{\omega}
\right ]\end{displaymath}](img261.gif) |
(20) |
![\begin{displaymath}
\bar \Psi(t)= \int d\omega g(\omega) \frac{\cos \omega t}{\s...
...ac{\omega}{\Theta_D} + \lambda \frac{\Theta_D}
{\omega} \right]\end{displaymath}](img262.gif) |
(21) |
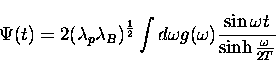 |
(22) |
In the literature the high temperature behavior is obtained by expanding Eq. (6.20) in a small region about t=0, which contains most of the contribution to the integral. However, this leads to the approximate expression
![\begin{displaymath}
1/\tau_c = \frac{2(\Delta_0 e^B)^2 {\pi}^{1/2}}{[(E+\gamma)T...
...{E}{T} + \frac{T}{E_B} -
\frac{T\xi_B^2}{16(E+\gamma)} \right]\end{displaymath}](img264.gif) |
(23) |
The integrals above are calculated here by numerical methods to yield
hop rates as a function of the dimensionless coupling constants
![]() , temperature and an overall scale factor
due to the normalization of the phonon spectrum.
Figure 6.26 shows the phonon density of states
, temperature and an overall scale factor
due to the normalization of the phonon spectrum.
Figure 6.26 shows the phonon density of states
![]() of solid Xe used in the numerical evaluation of
Eqs. (6.26, 6.27, 6.28),
adapted from data by Klein [59].
of solid Xe used in the numerical evaluation of
Eqs. (6.26, 6.27, 6.28),
adapted from data by Klein [59].
However, we shall need the measured hop rate before we can proceed with this calulation, so first we digress to the experiment.
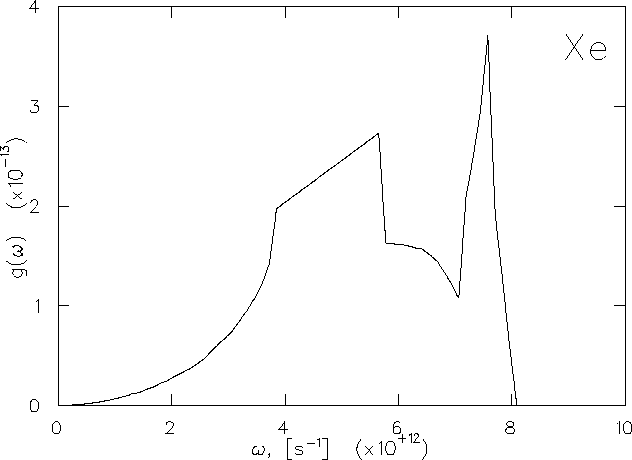 |