



Next: Spin ladder system
Up: 1.1 Antiferromagnetic spin systems
Previous: 1.1.1 An overview of
Historically, the `spin Peierls' system was the first macroscopic
system proposed to have a spin gap
[14,15,16]. It consists of an S=1/2
antiferromagnetic spin chain with a spin-lattice coupling. If the
lattice is soft in the chain direction, and the chains are magnetically
well separated from each other [17,18], a
periodic deformation (dimerization) of the lattice takes place at a
finite temperature 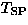 (Fig.3a
(Fig.3a b).
The lattice dimerization alternatively enhances [
b).
The lattice dimerization alternatively enhances [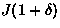 ] or
reduces [
] or
reduces [ ] the antiferromagnetic interactions, and brings
about singlet pair formations on the enhanced exchange links (Fig.3b).
] the antiferromagnetic interactions, and brings
about singlet pair formations on the enhanced exchange links (Fig.3b).
Figure 3:
(a) An S=1/2 spin chain with an uniform antiferromagnetic interaction J.
(b) The lattice dimerized state below the spin Peierls transition temperature 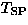 .
.
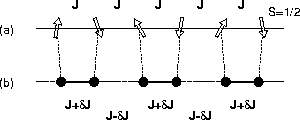 |
The ground state structure of the spin-Peierls system is a stacking of
singlet pairs along the chain. The ground state is non-magnetic, because
each singlet pair produces no magnetic field. Since the singlet
pairs are well localized, there is a finite energy gap between the ground
state and the excited states. This system is studied in Chapter 6.




Next: Spin ladder system
Up: 1.1 Antiferromagnetic spin systems
Previous: 1.1.1 An overview of

