

Next: BCS Theory for Conventional Superconductors
Up: Magnetic Properties of Conventional Superconductors
Previous: Ginzburg-Landau Theory
The purity of a superconductor is characterized by the ratio
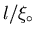 .
.
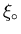 is the coherence length of the pure material, and is given by
Eq. (2.4). l is the electron mean free path, defined as:
is the coherence length of the pure material, and is given by
Eq. (2.4). l is the electron mean free path, defined as:
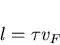 |
(9) |
where 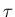 is the time interval between collisions of
conduction electrons with
impurities in the sample. The magnitude of
is the time interval between collisions of
conduction electrons with
impurities in the sample. The magnitude of 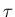 is determined in the
normal state. A sample is clean if
is determined in the
normal state. A sample is clean if
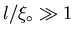 ,
and dirty
if
,
and dirty
if
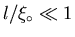 [20]. The actual coherence length when
impurities are considered, is dependent upon the mean free path l.
Intuitively, one can define an effective coherence length
[20]. The actual coherence length when
impurities are considered, is dependent upon the mean free path l.
Intuitively, one can define an effective coherence length
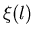 such that [13,17]:
such that [13,17]:
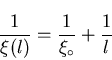 |
(10) |
According to Eq. (2.10), the coherence length 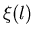 becomes
shorter with decreasing l, so that in the dirty limit:
becomes
shorter with decreasing l, so that in the dirty limit:
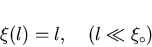 |
(11) |
and in the clean limit:
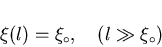 |
(12) |
Eq. (2.11) and Eq. (2.12) are valid only for T=0K.
In the clean limit (
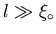 )
at T=0K, the magnetic penetration
depth is
the London penetration depth given in
Eq. (2.1). The actual
coherence length
)
at T=0K, the magnetic penetration
depth is
the London penetration depth given in
Eq. (2.1). The actual
coherence length 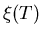 and the observed penetration depth
and the observed penetration depth
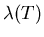 as determined by microscopic theory are given in the clean limit
(
as determined by microscopic theory are given in the clean limit
(
 )
as [21]:
)
as [21]:
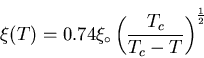 |
(13) |
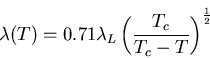 |
(14) |
and in the dirty limit (
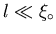 ):
):
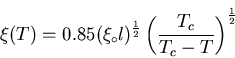 |
(15) |
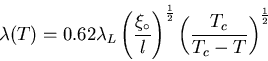 |
(16) |
where Equations (2.13) through (2.16)
are valid only in the neighborhood of Tc,
such that
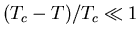 [22].
The important result is that according to Eqs.(2.15) and
(2.16), as l decreases (i.e. the superconductor becomes
more impure),
[22].
The important result is that according to Eqs.(2.15) and
(2.16), as l decreases (i.e. the superconductor becomes
more impure),
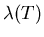 increases, while
increases, while 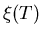 decreases. Thus
decreases. Thus
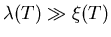 at all temperatures in an impure material. The
high-temperature superconductors have short coherence lengths on the
order of
at all temperatures in an impure material. The
high-temperature superconductors have short coherence lengths on the
order of
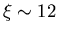 to 15Å. Since the electron mean free path
l is typically
to 15Å. Since the electron mean free path
l is typically 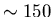 Å in these materials, then they are well
within the clean limit [23].
Å in these materials, then they are well
within the clean limit [23].



Next: BCS Theory for Conventional Superconductors
Up: Magnetic Properties of Conventional Superconductors
Previous: Ginzburg-Landau Theory
Jess H. Brewer
2001-09-28
![]() .
.
![]() is the coherence length of the pure material, and is given by
Eq. (2.4). l is the electron mean free path, defined as:
is the coherence length of the pure material, and is given by
Eq. (2.4). l is the electron mean free path, defined as: