


Next: The Clean and Dirty Limits
Up: Magnetic Properties of Conventional Superconductors
Previous: The Coherence Length (Pippard's Equation)
In 1950, Ginzburg and Landau introduced the so-called superconducting
order parameter
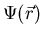 to describe the nonlocality of the
superconducting properties.
to describe the nonlocality of the
superconducting properties.
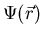 can be thought of as a
measure of the order in the superconducting state at position
can be thought of as a
measure of the order in the superconducting state at position 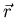 below Tc. It has the properties that
below Tc. It has the properties that
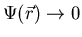 as
as
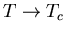 ,
and
,
and
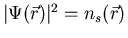 (i.e. the local density of superconducting electrons). At the time
Ginzburg-Landau (GL) theory was developed, the nature of the superconducting
carriers was yet to be determined. Interpreting m* as the
effective mass and q as the charge of the
fundamental superconducting particles (whatever they
may be), they derived the penetration depth as:
(i.e. the local density of superconducting electrons). At the time
Ginzburg-Landau (GL) theory was developed, the nature of the superconducting
carriers was yet to be determined. Interpreting m* as the
effective mass and q as the charge of the
fundamental superconducting particles (whatever they
may be), they derived the penetration depth as:
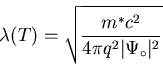 |
(6) |
where
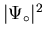 is the value of
is the value of
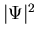 deep inside the superconductor (i.e. its equilibrium value). The
coherence length defined in the GL-formalism is:
deep inside the superconductor (i.e. its equilibrium value). The
coherence length defined in the GL-formalism is:
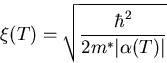 |
(7) |
where 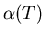 is a temperature-dependent
coefficient in the series expansion of the free energy (see [19]).
As written, (2.6) and (2.7)
suggest that the penetration
depth
is a temperature-dependent
coefficient in the series expansion of the free energy (see [19]).
As written, (2.6) and (2.7)
suggest that the penetration
depth
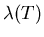 and the coherence length
and the coherence length 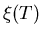 are
temperature dependent quantities.
Eq. (2.7) is closely related to the Pippard coherence
length
are
temperature dependent quantities.
Eq. (2.7) is closely related to the Pippard coherence
length
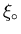 defined in Eq. (2.4).
In GL-theory, the coherence length
defined in Eq. (2.4).
In GL-theory, the coherence length 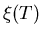 is the characteristic length for variations in
is the characteristic length for variations in
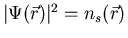 .
One noteable difference is that Pippard's coherence
length
.
One noteable difference is that Pippard's coherence
length
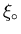 is independent of temperature. In fact in the
dirty limit
is independent of temperature. In fact in the
dirty limit 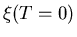 reduces to Eq. (2.4).
Near the transition temperature
Tc both
reduces to Eq. (2.4).
Near the transition temperature
Tc both
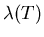 and
and 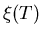 vary
as
(1-T/Tc)-1/2, prompting the introduction of the
Ginzburg-Landau parameter
vary
as
(1-T/Tc)-1/2, prompting the introduction of the
Ginzburg-Landau parameter 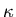 ,
where:
,
where:
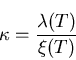 |
(8) |
The variation of
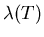 and
and 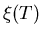 with temperture near Tccomes from an expansion of the free energy density to first-order in
the field
with temperture near Tccomes from an expansion of the free energy density to first-order in
the field 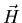 .
It follows that
.
It follows that 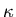 in (2.8)
is temperature
independent to this order. An exact calculation from microscopic theory
gives a weak temperature dependence for
in (2.8)
is temperature
independent to this order. An exact calculation from microscopic theory
gives a weak temperature dependence for 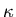 ,
with
,
with 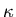 increasing for decreasing temperature T.
Through energy considerations, Ginzburg and Landau
characterized a type-I superconductor
as one in which
increasing for decreasing temperature T.
Through energy considerations, Ginzburg and Landau
characterized a type-I superconductor
as one in which
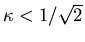 .
For
.
For
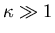 ,
GL theory
reduces to the London model.
,
GL theory
reduces to the London model.



Next: The Clean and Dirty Limits
Up: Magnetic Properties of Conventional Superconductors
Previous: The Coherence Length (Pippard's Equation)
Jess H. Brewer
2001-09-28
![]() to describe the nonlocality of the
superconducting properties.
to describe the nonlocality of the
superconducting properties.
![]() can be thought of as a
measure of the order in the superconducting state at position
can be thought of as a
measure of the order in the superconducting state at position ![]() below Tc. It has the properties that
below Tc. It has the properties that
![]() as
as
![]() ,
and
,
and
![]() (i.e. the local density of superconducting electrons). At the time
Ginzburg-Landau (GL) theory was developed, the nature of the superconducting
carriers was yet to be determined. Interpreting m* as the
effective mass and q as the charge of the
fundamental superconducting particles (whatever they
may be), they derived the penetration depth as:
(i.e. the local density of superconducting electrons). At the time
Ginzburg-Landau (GL) theory was developed, the nature of the superconducting
carriers was yet to be determined. Interpreting m* as the
effective mass and q as the charge of the
fundamental superconducting particles (whatever they
may be), they derived the penetration depth as: