 |
Superconductivity refers to the unusual electrical and magnetic behaviour
exhibited by certain materials below their critical temperature Tc,
usually near absolute zero. These phenomena include negligible resistance to
electric current and the expulsion of external magnetic fields, and
find application in Magnetic Resonance Imaging (MRI) and high capacity power
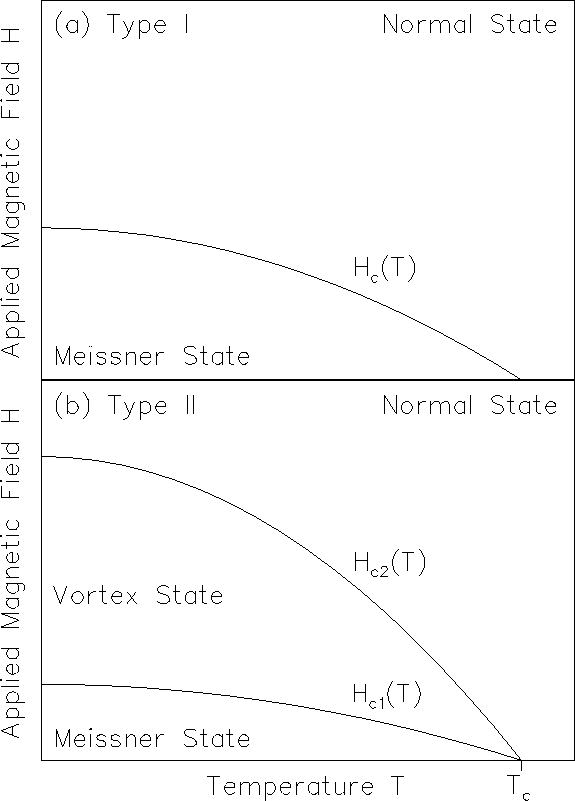
transmission cables. Based on their response to the applied
magnetic field H, superconductors fall into two major classes, type I and
type II, as illustrated in Figure 1.1.
This thesis focusses on the behaviour of the vortex core radius ![]() as a
function of temperature T in LuNi2B2C, as studied with muon spin
rotation (
as a
function of temperature T in LuNi2B2C, as studied with muon spin
rotation (![]() SR) spectroscopy. (For a discussion of the field dependence,
see [2].) Whereas the core radius
SR) spectroscopy. (For a discussion of the field dependence,
see [2].) Whereas the core radius ![]() is often assumed to remain
constant at low temperatures
is often assumed to remain
constant at low temperatures ![]() ,
theoretical works [3][4][5]
propose that the core radius
,
theoretical works [3][4][5]
propose that the core radius ![]() should
contract linearly with falling temperature
should
contract linearly with falling temperature ![]() ,
and stop shrinking
at a quantum limit temperature T0, where the radius
,
and stop shrinking
at a quantum limit temperature T0, where the radius ![]() is on the order
of a Fermi
wavelength. Experimental confirmation of such a temperature dependence,
known as the Kramer-Pesch effect, would
necessitate a reconsideration of the common assumption that the radius
is on the order
of a Fermi
wavelength. Experimental confirmation of such a temperature dependence,
known as the Kramer-Pesch effect, would
necessitate a reconsideration of the common assumption that the radius ![]() remains constant at low temperatures. To date,
remains constant at low temperatures. To date, ![]() SR
observations [6][7] of the
core radius
SR
observations [6][7] of the
core radius ![]() have revealed only a fairly weak
Kramer-Pesch effect. These experiments dealt with quasi two-dimensional
materials, introducing the possibility of systematic overestimation of the
core radius
have revealed only a fairly weak
Kramer-Pesch effect. These experiments dealt with quasi two-dimensional
materials, introducing the possibility of systematic overestimation of the
core radius ![]() as a result of longitudinal disorder of
vortices [7]. This complication has much less impact in the case
of LuNi2B2C, a member of a new family of materials that exhibit unusual
superconducting behaviour, because LuNi2B2C is nearly isotropic. This
superconductor is thus a prime candidate with which to see the
predicted Kramer-Pesch effect.
as a result of longitudinal disorder of
vortices [7]. This complication has much less impact in the case
of LuNi2B2C, a member of a new family of materials that exhibit unusual
superconducting behaviour, because LuNi2B2C is nearly isotropic. This
superconductor is thus a prime candidate with which to see the
predicted Kramer-Pesch effect.
This thesis proceeds as follows. The next chapter outlines basic relevant
superconductivity concepts, and
goes into detail about the expected Kramer-Pesch effect and previous
experimental results concerning it. A general overview of the
properties of LuNi2B2C appears in Chapter 3, along with a
quantitative estimate of the Kramer-Pesch effect anticipated for this
superconductor. Chapter 4 describes the transverse field
![]() SR technique and the experimental setup. Chapter 5 explains
how the time dependent muon polarisation signal
P(t) is fitted to a
nonlocal
London model developed for borocarbides, and how the core radius
SR technique and the experimental setup. Chapter 5 explains
how the time dependent muon polarisation signal
P(t) is fitted to a
nonlocal
London model developed for borocarbides, and how the core radius ![]() is calculated from the fitted internal magnetic field
profile
B(r). It also examines the quality of the fits
as a function of the penetration depth
is calculated from the fitted internal magnetic field
profile
B(r). It also examines the quality of the fits
as a function of the penetration depth ![]() ,
the nonlocality
parameter C and the
core radius
,
the nonlocality
parameter C and the
core radius ![]() .
Chapter 6 presents the resulting temperature
dependence of the fitted penetration depth
.
Chapter 6 presents the resulting temperature
dependence of the fitted penetration depth ![]() and nonlocality
parameter C,
and the extracted core radius
and nonlocality
parameter C,
and the extracted core radius ![]() ,
for LuNi2B2C under a constant
applied field of
,
for LuNi2B2C under a constant
applied field of
![]() .
It compares the low temperature
behaviour of
the core radius
.
It compares the low temperature
behaviour of
the core radius ![]() measured in LuNi2B2C with the predicted
Kramer-Pesch effect, as well as the core radius temperature
dependences
measured in LuNi2B2C with the predicted
Kramer-Pesch effect, as well as the core radius temperature
dependences ![]() observed previously in NbSe2 and
YBaCu3O
observed previously in NbSe2 and
YBaCu3O
![]() under an applied field
under an applied field
![]() .
This
chapter also contrasts the internal magnetic field distributions n(B) of
the nonlocal and local London models. Finally, Chapter 7
summarises these results and their implications.
.
This
chapter also contrasts the internal magnetic field distributions n(B) of
the nonlocal and local London models. Finally, Chapter 7
summarises these results and their implications.