



Next: Fast Fourier Transform (FFT)
Up: SR Spectroscopy
Previous: Time Differential SR (TD-SR)
Contents
In a transverse-field muon spin rotation experiment (Fig. 2.3), a magnetic field 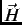 is applied
perpendicular to the initial muon-spin polarization direction. A muon stopping in the sample Larmor precesses about the
local magnetic field
is applied
perpendicular to the initial muon-spin polarization direction. A muon stopping in the sample Larmor precesses about the
local magnetic field 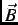 (which in general is different than the external field) at an angular frequency
(which in general is different than the external field) at an angular frequency
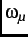 =
=
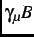 , where
, where
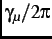 =
= 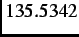 MHzT
MHzT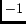 is the muon gyromagnetic ratio.
is the muon gyromagnetic ratio.
Fig. 2.3:
Schematic diagram of a TF- SR experiment. The initial muon spin
polarization
SR experiment. The initial muon spin
polarization
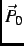 , indicated by the open arrow at
, indicated by the open arrow at 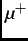 , is rotated by 90
, is rotated by 90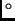 so that it is perpendicular
to the direction of the external magnetic field
so that it is perpendicular
to the direction of the external magnetic field 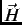 . The open arrows at the sample S illustrate the Larmor
precession of the muon spin.
. The open arrows at the sample S illustrate the Larmor
precession of the muon spin.
|
|
In a superconductor the muons stop at well defined sites in the crystal lattice. However, in the vortex state of a type-II
superconductor, the muons stop randomly on the length scale of the vortex lattice (which is typically two to three orders of
magnitude larger than that of the crystal lattice). Consequently, 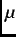 SR is an effective local probe of the spatial
variation of internal magnetic fields due to the periodic arrangement of vortices. For the case where the external field is
directed along
SR is an effective local probe of the spatial
variation of internal magnetic fields due to the periodic arrangement of vortices. For the case where the external field is
directed along 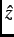 , the
, the  component of the muon-spin polarization function is
component of the muon-spin polarization function is
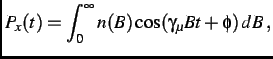 |
(3.6) |
where 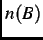 is the probability that a muon sees a local magnetic field between
is the probability that a muon sees a local magnetic field between 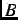 and
and 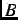 +
+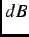 , and
, and 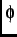 is the initial
phase. There are several sources of the local magnetic field sensed by the muons. First there is the magnetic field
inhomogeneity associated with the vortex lattice. For a type-II superconductor, the spatial profile of the magnetic field
in the
is the initial
phase. There are several sources of the local magnetic field sensed by the muons. First there is the magnetic field
inhomogeneity associated with the vortex lattice. For a type-II superconductor, the spatial profile of the magnetic field
in the 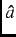 -
-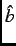 plane due to an applied field along the
plane due to an applied field along the 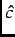 axis (
axis (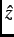 direction) is reasonably
described by the phenomenological model [19]
direction) is reasonably
described by the phenomenological model [19]
 |
(3.7) |
where 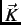 is a reciprocal lattice vector,
is a reciprocal lattice vector, 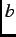 =
=
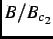 is the reduced field,
is the reduced field, 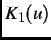 is a modified Bessel
function and
is a modified Bessel
function and 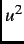 =
=
![$ 2\xi_{ab}K^2(1+b^4)[1-2b(1-b)^2]$](img141.png) . Equation (2.7), which is derived from Ginzburg-Landau
theory, assumes that
. Equation (2.7), which is derived from Ginzburg-Landau
theory, assumes that
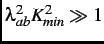 , where
, where
 is the magnitude of the smallest non-zero
reciprocal-lattice vector in the summation. This condition is satisfied for an extreme type-II superconductor like the
high-
is the magnitude of the smallest non-zero
reciprocal-lattice vector in the summation. This condition is satisfied for an extreme type-II superconductor like the
high- cuprates, where
cuprates, where
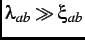 . This self-consistent analytic function, agrees extremely well with
the exact numerical solutions of the Ginzburg-Landau equations at low reduced fields
. This self-consistent analytic function, agrees extremely well with
the exact numerical solutions of the Ginzburg-Landau equations at low reduced fields 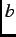 . Random vortex pinning and thermal
fluctuations modify the field distribution associated with Eq. (2.7), which assumes a perfect periodic
arrangement of vortices.
. Random vortex pinning and thermal
fluctuations modify the field distribution associated with Eq. (2.7), which assumes a perfect periodic
arrangement of vortices.
The muon is also sensitive to both nuclear and electronic dipole moments. The nuclear moments are randomly oriented at
temperatures reachable in a 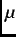 SR experiment (i.e.
SR experiment (i.e. 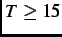 mK), whereas electronic magnetic moments may order.
In general, the magnetic moments that are static on the
mK), whereas electronic magnetic moments may order.
In general, the magnetic moments that are static on the 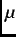 SR time scale broaden the measured internal magnetic field
distribution. To account for the effects of this additional source of field inhomomgeneity on the muon-spin polarization
function, Eq. (2.6) can be multiplied by a depolarization function
SR time scale broaden the measured internal magnetic field
distribution. To account for the effects of this additional source of field inhomomgeneity on the muon-spin polarization
function, Eq. (2.6) can be multiplied by a depolarization function 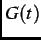 such that
such that
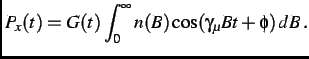 |
(3.8) |
The precise functional form of 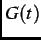 depends on the nature of the additional sources of magnetic field at the muon site.
For example, a Gaussian function
depends on the nature of the additional sources of magnetic field at the muon site.
For example, a Gaussian function 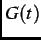 =
=
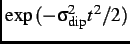 with a depolarization rate
with a depolarization rate
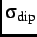 , characterizes the damping of the muon-spin precession signal due to dense static dipole moments [20].
, characterizes the damping of the muon-spin precession signal due to dense static dipole moments [20].




Next: Fast Fourier Transform (FFT)
Up: SR Spectroscopy
Previous: Time Differential SR (TD-SR)
Contents
Jess H. Brewer
2003-07-01
![\includegraphics[width=12cm]{TF-muSR.eps}](img124.png)
![]() SR is an effective local probe of the spatial
variation of internal magnetic fields due to the periodic arrangement of vortices. For the case where the external field is
directed along
SR is an effective local probe of the spatial
variation of internal magnetic fields due to the periodic arrangement of vortices. For the case where the external field is
directed along ![]() , the
, the ![]() component of the muon-spin polarization function is
component of the muon-spin polarization function is
![]() SR experiment (i.e.
SR experiment (i.e. ![]() mK), whereas electronic magnetic moments may order.
In general, the magnetic moments that are static on the
mK), whereas electronic magnetic moments may order.
In general, the magnetic moments that are static on the ![]() SR time scale broaden the measured internal magnetic field
distribution. To account for the effects of this additional source of field inhomomgeneity on the muon-spin polarization
function, Eq. (2.6) can be multiplied by a depolarization function
SR time scale broaden the measured internal magnetic field
distribution. To account for the effects of this additional source of field inhomomgeneity on the muon-spin polarization
function, Eq. (2.6) can be multiplied by a depolarization function ![]() such that
such that