



Next: Experimental Details
Up: SR Spectroscopy
Previous: Fast Fourier Transform (FFT)
Contents
One of the advantages of 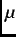 SR spectroscopy over other magnetic resonance techniques (i.e. NMR, ESR) is that
measurements can be performed in zero external magnetic field. In a zero-field muon-spin relaxation (ZF-
SR spectroscopy over other magnetic resonance techniques (i.e. NMR, ESR) is that
measurements can be performed in zero external magnetic field. In a zero-field muon-spin relaxation (ZF-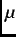 SR)
experiment (Fig. 2.4), muons are used to probe the local magnetic field at their stopping site due to nearby
nuclear and/or electronic magnetic moments. This is achieved by measuring the time evolution of the muon-spin polarization
along its original direction (i.e. the relaxation function).
SR)
experiment (Fig. 2.4), muons are used to probe the local magnetic field at their stopping site due to nearby
nuclear and/or electronic magnetic moments. This is achieved by measuring the time evolution of the muon-spin polarization
along its original direction (i.e. the relaxation function).
Fig. 2.4:
Schematic diagram of a ZF-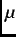 SR experiment.
SR experiment.
|
|
If the local magnetic fields are static, the muon will Larmor precess about the component of local field that is
perpendicular to the muon spin. For the case of a sample with magnetic order, this gives rise to a muon-spin precession
signal with a discrete frequency oscillation for each magnetically inequivalent muon site in the crystallographic lattice.
The observed ZF relaxation function is
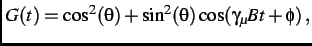 |
(3.11) |
where 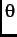 is the angle between the muon spin and the average static internal field
is the angle between the muon spin and the average static internal field 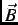 .
.
The magnetic field distribution sensed by the muons in a system consisting of dense randomly oriented static magnetic
moments is a Gaussian function. The corresponding relaxation function is given by the famous (Gaussian) Kubo-Toyabe (KT)
function [21]
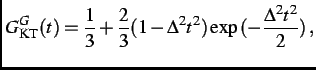 |
(3.12) |
where 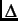 is the relaxation rate and
is the relaxation rate and
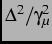 is the width of the magnetic field distribution at
the muon site. Note that for early times (
is the width of the magnetic field distribution at
the muon site. Note that for early times (
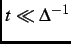 ) or for slow relaxation, Eq. (2.12) can be
Taylor expanded as
) or for slow relaxation, Eq. (2.12) can be
Taylor expanded as
The Gaussian KT function is routinely used to describe nuclear magnetic moments, which are static on the 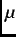 SR time scale.
SR time scale.
A Lorentzian magnetic field distribution is sensed by the muons in a system consisting of dilute randomly oriented static
magnetic moments (i.e. moments that are distributed randomly on less than 1% of the lattice sites). The corresponding
relaxation function is a Lorentzian KT function [22]
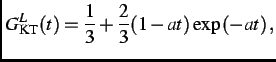 |
(3.14) |
where 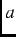 is the relaxation rate. For early times (
is the relaxation rate. For early times (
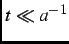 ) or for slow relaxation, Eq. (2.14) can
be Taylor expanded as
) or for slow relaxation, Eq. (2.14) can
be Taylor expanded as
where 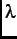 =
= 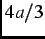 is the relaxation rate. The above KT functions describe dense/dilute randomly oriented static
magnetic moments. For the situation where the local magnetism is intermediate between the dilute and dense limits, or dilute
electronic magnetic moments (or magnetic clusters) are embedded in a system of concentrated nuclear dipoles, some
combination of Eq. (2.13) and Eq. (2.15) is required.
is the relaxation rate. The above KT functions describe dense/dilute randomly oriented static
magnetic moments. For the situation where the local magnetism is intermediate between the dilute and dense limits, or dilute
electronic magnetic moments (or magnetic clusters) are embedded in a system of concentrated nuclear dipoles, some
combination of Eq. (2.13) and Eq. (2.15) is required.
If the magnetic moments in the sample are slowly fluctuating i.e.
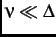 where
where 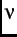 is the fluctuation
rate, the ``
is the fluctuation
rate, the ``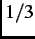 tail'' in the KT functions relax to zero. If the magnetic moments are fluctuating at a high rate such that
tail'' in the KT functions relax to zero. If the magnetic moments are fluctuating at a high rate such that
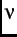 >
> 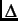 , the relaxation function then becomes an exponential function
, the relaxation function then becomes an exponential function
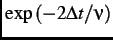 . For intermediate
values of
. For intermediate
values of 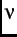 , the relaxation function has no analytical form.
, the relaxation function has no analytical form.




Next: Experimental Details
Up: SR Spectroscopy
Previous: Fast Fourier Transform (FFT)
Contents
Jess H. Brewer
2003-07-01
![]() where
where ![]() is the fluctuation
rate, the ``
is the fluctuation
rate, the ``![]() tail'' in the KT functions relax to zero. If the magnetic moments are fluctuating at a high rate such that
tail'' in the KT functions relax to zero. If the magnetic moments are fluctuating at a high rate such that
![]() >
> ![]() , the relaxation function then becomes an exponential function
, the relaxation function then becomes an exponential function
![]() . For intermediate
values of
. For intermediate
values of ![]() , the relaxation function has no analytical form.
, the relaxation function has no analytical form.