



Next: .
Up: 6.1 Introduction
Previous: Structural investigations [#!MonctonPRL77!#,#!vanBodegomPRB81!#]
Since the first excited state of the spin Peierls phase is the triplet
state, one can close the spin Peierls energy gap by applying a large
magnetic field. Experimentally, high-field magnetization measurements
[133,134,135] have detected this signature.
At  , the magnetization M(H) remained small up to a
critical field (Hc), and above Hc, it linearly increased. This
experimental result indicates that one branch of the triplet
states crosses levels with the singlet ground state at
the critical field Hc.
, the magnetization M(H) remained small up to a
critical field (Hc), and above Hc, it linearly increased. This
experimental result indicates that one branch of the triplet
states crosses levels with the singlet ground state at
the critical field Hc.
Figure:
Phase diagram of spin Peierls systems. Temperature (T) and magnetic
field (H) are normalized with  . Cite from Ref. [139].
. Cite from Ref. [139].
 |
High-field magnetization measurements have provided the phase diagram
of spin Peierls materials as shown in Fig.51.
It was found that the phase boundaries fall on universal curves, if
temperature (T) and magnetic field (H) were normalized with
 , which is the spin-Peierls transition
temperature in zero-field [135]. From the hysteresis of
magnetization [135], the phase boundary between the
spin-Peierls phase (SP) and the magnetic phase (M
, which is the spin-Peierls transition
temperature in zero-field [135]. From the hysteresis of
magnetization [135], the phase boundary between the
spin-Peierls phase (SP) and the magnetic phase (M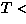 ) was found to
be first-order. The phase boundary between the uniform phase (U) and
other phases (SP and M
) was found to
be first-order. The phase boundary between the uniform phase (U) and
other phases (SP and M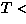 ) is second order. This boundary is well
described with a theoretical curve [140] obtained from
Cross and Fisher's approach.
) is second order. This boundary is well
described with a theoretical curve [140] obtained from
Cross and Fisher's approach.
As a microscopic structure of the M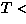 phase, a localized spin
state (spin soliton) has been proposed theoretically
[126]. If this localized spin state is realized, the local
field at a certain position of the crystalline unit cell should have a
relatively broad distribution, because the spin soliton is spatially
inhomogeneous. From an investigation of the 1H- and 19F-NMR
line-shape [136] and ESR line-shift [137],
the existence of spin solitons was experimentally suggested in the
M
phase, a localized spin
state (spin soliton) has been proposed theoretically
[126]. If this localized spin state is realized, the local
field at a certain position of the crystalline unit cell should have a
relatively broad distribution, because the spin soliton is spatially
inhomogeneous. From an investigation of the 1H- and 19F-NMR
line-shape [136] and ESR line-shift [137],
the existence of spin solitons was experimentally suggested in the
M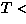 phase of TTF-AuBDT.
phase of TTF-AuBDT.
Theoretically, the spin soliton is accompanied by
incommensurate lattice modulations; in the vicinity of a spin
soliton, the lattice dimerization should be lifted. Recently,
Kiryukhin et al. performed high-resolution X-ray diffraction
measurements on TTF-CuBDT, and found the incommensurate modulations of
the lattice appearing in the M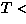 phase [138].
phase [138].




Next: .
Up: 6.1 Introduction
Previous: Structural investigations [#!MonctonPRL77!#,#!vanBodegomPRB81!#]
![]() phase, a localized spin
state (spin soliton) has been proposed theoretically
[126]. If this localized spin state is realized, the local
field at a certain position of the crystalline unit cell should have a
relatively broad distribution, because the spin soliton is spatially
inhomogeneous. From an investigation of the 1H- and 19F-NMR
line-shape [136] and ESR line-shift [137],
the existence of spin solitons was experimentally suggested in the
M
phase, a localized spin
state (spin soliton) has been proposed theoretically
[126]. If this localized spin state is realized, the local
field at a certain position of the crystalline unit cell should have a
relatively broad distribution, because the spin soliton is spatially
inhomogeneous. From an investigation of the 1H- and 19F-NMR
line-shape [136] and ESR line-shift [137],
the existence of spin solitons was experimentally suggested in the
M![]() phase of TTF-AuBDT.
phase of TTF-AuBDT.
![]() phase [138].
phase [138].