



Next: Concluding remarks
Up: Discussion and Conclusion
Previous: Condensed matter and subthreshold
Using the emitted beam of  from a hydrogen layer,
we have measured
the formation rates and resonance energy of
from a hydrogen layer,
we have measured
the formation rates and resonance energy of 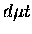 muonic molecules. The
combined results of the rate and energy scaling parameters
muonic molecules. The
combined results of the rate and energy scaling parameters
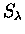 ,
SE from two separate sets of runs are:
,
SE from two separate sets of runs are:
where the first errors are experimental uncertainties and
the second ones are MC modeling uncertainties (including target geometry).
When the errors are added in quadrature, we have achieved accuracies of
about 25% and 10% respectively for the formation rates and energy. Our
measurement of resonant molecular formation corresponds to a peak
rate![[*]](foot_motif.gif) of
of
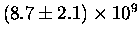 s-1 for the reaction
s-1 for the reaction
quantitatively confirming for the first
time the existence of the strong epithermal resonance.
Our measurement of the resonance energy scaling corresponds to the position
for the strongest the resonance peak in the reaction
(9.6) of
meV in the  lab frame. If
we assume the molecular spectrum of the complex [
lab frame. If
we assume the molecular spectrum of the complex [
 ]
is
predicted reliably, our results can be considered a first direct
measurement of the loosely bound state energy level. Our accuracy of
meV in the center of mass frame, compared to the muonic atomic energy
scale [2] of
=
=
eV,
is better than 10 ppm. Indeed it is comparable to the vacuum polarization
correction in the loosely bound state energy level.
]
is
predicted reliably, our results can be considered a first direct
measurement of the loosely bound state energy level. Our accuracy of
meV in the center of mass frame, compared to the muonic atomic energy
scale [2] of
=
=
eV,
is better than 10 ppm. Indeed it is comparable to the vacuum polarization
correction in the loosely bound state energy level.
Until a few years ago, the problem of muonic molecule binding energies
appeared to have been completely settled at least for the 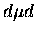 case.
Extraction of the binding energy from the temperature dependence of
case.
Extraction of the binding energy from the temperature dependence of 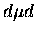 formation rates, as analyzed by Scrinzi et al. [12], showed
remarkable agreement with the theoretical prediction. However, new studies,
both theoretical and experimental, seem to indicate the real situation is
not as clear. For example, recent calculations by Harston et al. on
the
formation rates, as analyzed by Scrinzi et al. [12], showed
remarkable agreement with the theoretical prediction. However, new studies,
both theoretical and experimental, seem to indicate the real situation is
not as clear. For example, recent calculations by Harston et al. on
the 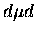 finite size effects indicates that previous values used in
Ref. [12] were significantly underestimated. Similar effects are
suggested for the
finite size effects indicates that previous values used in
Ref. [12] were significantly underestimated. Similar effects are
suggested for the 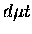 case by Bakalov et al. [137].
Experimentally, new and precise measurements of
case by Bakalov et al. [137].
Experimentally, new and precise measurements of 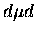 fusion at
PSI [236] are not in complete agreement with those used in
Ref. [12]. In addition, the assumption of complete
fusion at
PSI [236] are not in complete agreement with those used in
Ref. [12]. In addition, the assumption of complete 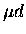 thermalization may not be valid at low temperatures. It should also be
stressed that in the
thermalization may not be valid at low temperatures. It should also be
stressed that in the 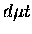 case, because of the lack of experimental
observation of the temperature dependence predicted by the standard Vesman
theory, there was virtually no experimental information on the
case, because of the lack of experimental
observation of the temperature dependence predicted by the standard Vesman
theory, there was virtually no experimental information on the 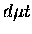 energy level. Thus our measurements of the resonance energy may provide an
interesting new opportunity to test the calculations of
energy level. Thus our measurements of the resonance energy may provide an
interesting new opportunity to test the calculations of 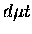 binding
energies.
binding
energies.
Let us make a few remarks on the theoretical assumptions in our
analysis.
- Inclusion of explicit back decay in the simulation is essential. The
use
of the renormalized effective rates without an explicit resonant
scattering channel would lead to a significant overestimate in the
calculated fusion yield. See appendix B for a detailed discussion.
- In our Monte Carlo simulations, the dependence of the formation rates
and fusion probability W on the quantum states S,
Kf are separately averaged, i.e., the averages for
and W over the quantum states are
factorized
![[*]](foot_motif.gif) . This is not rigorously accurate if the
their dependence on S or Kf is large. Although this is probably not a
large effect, the precise estimate of the degree of accuracy requires
comparisons with more complete calculations.
. This is not rigorously accurate if the
their dependence on S or Kf is large. Although this is probably not a
large effect, the precise estimate of the degree of accuracy requires
comparisons with more complete calculations.
- Since our D2 target is not in thermal equilibrium rotationally
(i.e.,
) the use of
Eq. 2.40-2.42 assuming the Boltzmann
distribution for Kf may introduce some error, though judging from the
difference in the results between using
Eq. 2.40-2.42 and
Eq. 2.37-2.39 at 300 K, shown in Figs. 10 and 11
of Ref. [133], the effects appear rather small. The Kfdistribution could also be affected if the rotational relaxation is
substantially smaller than predicted by Ostrovskii and
Ustimov [153], as suggested in Ref. [154].
- The use of a (state independent) effective fusion rate
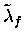 appears valid at least for its Auger decay contribution, since it
is presumably independent of
,
or S. However the value
used,
s-1, could be
overestimated by %, if the lowest value amongst Armour's
several predictions [152] turns out to be the correct
one. This would not affect low energy formation where the fusion
probability is very high, but could have a significant effect in
epithermal formation, where fusion and back decay branches are
comparable. On the other hand, possible collisional vibrational
quenching would increase
appears valid at least for its Auger decay contribution, since it
is presumably independent of
,
or S. However the value
used,
s-1, could be
overestimated by %, if the lowest value amongst Armour's
several predictions [152] turns out to be the correct
one. This would not affect low energy formation where the fusion
probability is very high, but could have a significant effect in
epithermal formation, where fusion and back decay branches are
comparable. On the other hand, possible collisional vibrational
quenching would increase
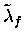 .
.
- Our method of scaling the formation rate, given
in Eq. 8.8,
while keeping the fusion probability W fixed, is phenomenological in
nature. More physically motivated scaling would be to scale the matrix
elements, which change both
and W. By the same token,
scaling of the
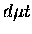 binding energy as input into the formation rate
calculations, and comparisons with the resulting resonance structures
(assuming scaled binding energies) may be more justified than our simple
scaling in Eq. 8.9 for the resonance energy
measurements, although these comparisons would require considerable input
from theorists. Thus, our scaling results should be taken as a first step
toward a more complete analysis.
binding energy as input into the formation rate
calculations, and comparisons with the resulting resonance structures
(assuming scaled binding energies) may be more justified than our simple
scaling in Eq. 8.9 for the resonance energy
measurements, although these comparisons would require considerable input
from theorists. Thus, our scaling results should be taken as a first step
toward a more complete analysis.
- In our analysis, the resonance width is given by Faifman et al.,
which is determined by the Doppler broadening due to the D2 motion
assuming a 3 K gas. In a solid, however, the Doppler broadening is expected
to be larger due in part to the larger zero-point motion of a D2 bound
in the lattice, hence the resonance profile may be broader. The precise
evaluation of this effect would require more theoretical work which is in
progress [170].
Finally, let us present in Fig. 9.3 a comparison of our
data with the MC calculations assuming a constant rate for 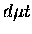 formation, a value of which was chosen to reproduce the fusion yield in the
US moderator layer. The indication is quite convincing; we have confirmed
the existence of epithermal resonant
formation, a value of which was chosen to reproduce the fusion yield in the
US moderator layer. The indication is quite convincing; we have confirmed
the existence of epithermal resonant 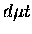 formation in
formation in  collisions with D2.
collisions with D2.




Next: Concluding remarks
Up: Discussion and Conclusion
Previous: Condensed matter and subthreshold
![]() from a hydrogen layer,
we have measured
the formation rates and resonance energy of
from a hydrogen layer,
we have measured
the formation rates and resonance energy of ![]() muonic molecules. The
combined results of the rate and energy scaling parameters
muonic molecules. The
combined results of the rate and energy scaling parameters
![]() ,
SE from two separate sets of runs are:
,
SE from two separate sets of runs are:
![[*]](foot_motif.gif) of
of
![]() lab frame. If
we assume the molecular spectrum of the complex [
lab frame. If
we assume the molecular spectrum of the complex [
![]() ]
is
predicted reliably, our results can be considered a first direct
measurement of the loosely bound state energy level. Our accuracy of
meV in the center of mass frame, compared to the muonic atomic energy
scale [2] of
=
=
eV,
is better than 10 ppm. Indeed it is comparable to the vacuum polarization
correction in the loosely bound state energy level.
]
is
predicted reliably, our results can be considered a first direct
measurement of the loosely bound state energy level. Our accuracy of
meV in the center of mass frame, compared to the muonic atomic energy
scale [2] of
=
=
eV,
is better than 10 ppm. Indeed it is comparable to the vacuum polarization
correction in the loosely bound state energy level.
![]() case.
Extraction of the binding energy from the temperature dependence of
case.
Extraction of the binding energy from the temperature dependence of ![]() formation rates, as analyzed by Scrinzi et al. [12], showed
remarkable agreement with the theoretical prediction. However, new studies,
both theoretical and experimental, seem to indicate the real situation is
not as clear. For example, recent calculations by Harston et al. on
the
formation rates, as analyzed by Scrinzi et al. [12], showed
remarkable agreement with the theoretical prediction. However, new studies,
both theoretical and experimental, seem to indicate the real situation is
not as clear. For example, recent calculations by Harston et al. on
the ![]() finite size effects indicates that previous values used in
Ref. [12] were significantly underestimated. Similar effects are
suggested for the
finite size effects indicates that previous values used in
Ref. [12] were significantly underestimated. Similar effects are
suggested for the ![]() case by Bakalov et al. [137].
Experimentally, new and precise measurements of
case by Bakalov et al. [137].
Experimentally, new and precise measurements of ![]() fusion at
PSI [236] are not in complete agreement with those used in
Ref. [12]. In addition, the assumption of complete
fusion at
PSI [236] are not in complete agreement with those used in
Ref. [12]. In addition, the assumption of complete ![]() thermalization may not be valid at low temperatures. It should also be
stressed that in the
thermalization may not be valid at low temperatures. It should also be
stressed that in the ![]() case, because of the lack of experimental
observation of the temperature dependence predicted by the standard Vesman
theory, there was virtually no experimental information on the
case, because of the lack of experimental
observation of the temperature dependence predicted by the standard Vesman
theory, there was virtually no experimental information on the ![]() energy level. Thus our measurements of the resonance energy may provide an
interesting new opportunity to test the calculations of
energy level. Thus our measurements of the resonance energy may provide an
interesting new opportunity to test the calculations of ![]() binding
energies.
binding
energies.
![[*]](foot_motif.gif) . This is not rigorously accurate if the
their dependence on S or Kf is large. Although this is probably not a
large effect, the precise estimate of the degree of accuracy requires
comparisons with more complete calculations.
. This is not rigorously accurate if the
their dependence on S or Kf is large. Although this is probably not a
large effect, the precise estimate of the degree of accuracy requires
comparisons with more complete calculations.
![]() formation, a value of which was chosen to reproduce the fusion yield in the
US moderator layer. The indication is quite convincing; we have confirmed
the existence of epithermal resonant
formation, a value of which was chosen to reproduce the fusion yield in the
US moderator layer. The indication is quite convincing; we have confirmed
the existence of epithermal resonant ![]() formation in
formation in ![]() collisions with D2.
collisions with D2.