



Next: Subthreshold resonances
Up: The standard Vesman model
Previous: Decay of the molecular
Total and effective formation rates
For our analysis, it is convenient to express the formation rates as a
function of the  laboratory (lab) energy, as opposed to the target
temperature given in Eq. 2.27. Specifying the initial
and final states, we then have
laboratory (lab) energy, as opposed to the target
temperature given in Eq. 2.27. Specifying the initial
and final states, we then have![[*]](foot_motif.gif) :
:
 |
(47) |
where
where
 is the initial rotational population distribution,
which for equilibrated targets is the standard Boltzmann distribution,
and Aif is a coefficient which depends on initial and final quantum
numbers. The factor
is the initial rotational population distribution,
which for equilibrated targets is the standard Boltzmann distribution,
and Aif is a coefficient which depends on initial and final quantum
numbers. The factor
 is the Doppler broadening
profile due to target motion and recoil, whose exact form is derived in
Ref. [133], but for
is the Doppler broadening
profile due to target motion and recoil, whose exact form is derived in
Ref. [133], but for
 can be
approximated [157] as a Gaussian distribution with the width of:
can be
approximated [157] as a Gaussian distribution with the width of:
 |
(50) |
In Eq. 2.35, a  function resonance profile was
assumed (the classical Vesman model), but even with that, the formation
rate in the lab frame has a distribution with non-zero width due to the
above-mentioned Doppler broadening.
function resonance profile was
assumed (the classical Vesman model), but even with that, the formation
rate in the lab frame has a distribution with non-zero width due to the
above-mentioned Doppler broadening.
At epithermal energies, the transition formation matrix elements
become very large, which means both the
formation rate and back decay width are large, resulting in a
significant probability for 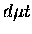 not fusing but returning to the
entrance channel
not fusing but returning to the
entrance channel
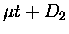 .
The effective formation rate is a renormalized rate taking into account the
fusion probability, as defined in Ref. [134]:
.
The effective formation rate is a renormalized rate taking into account the
fusion probability, as defined in Ref. [134]:
 |
(51) |
where
For a high density (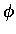 more than about 0.1) target such as ours,
Faifman assumes complete rotational relaxation of the Kf levels, hence
dropping the Kf dependence,
more than about 0.1) target such as ours,
Faifman assumes complete rotational relaxation of the Kf levels, hence
dropping the Kf dependence,
where
 is the Boltzmann distribution of the Kf states
is the Boltzmann distribution of the Kf states
![[*]](foot_motif.gif) .
.
The effective fusion probability for the
molecular complex is defined as [133]:
 |
(57) |
where
 is the rate for non-resonant formation,
which does not back-decay. For
is the rate for non-resonant formation,
which does not back-decay. For
 ,
WF can be written:
,
WF can be written:
 |
(58) |
which can be understood as the average of fusion probabilities from each
state weighted by the formation rate of that state.
Figure 2.4 shows the molecular formation rates
 and effective fusion probabilities WF for Ki=0(ortho) and Ki=1 (para) cases, calculated by Faifman et
al. [70,71,72] for a 3 K target. Also shown are
the effective rates
and effective fusion probabilities WF for Ki=0(ortho) and Ki=1 (para) cases, calculated by Faifman et
al. [70,71,72] for a 3 K target. Also shown are
the effective rates
 .
Note that
.
Note that
 less than about 107s-1 is invisible in the scale plotted.
less than about 107s-1 is invisible in the scale plotted.
Figure 2.4:
Formation rates
 for
for
![$\mu t + D_2
\rightarrow [(d\mu t)dee]^*$](img326.gif) (top) and the fusion probability WF(bottom), calculated by Faifman [70,71,72] for 3
K. Also shown in dashed lines are the effective rate
(top) and the fusion probability WF(bottom), calculated by Faifman [70,71,72] for 3
K. Also shown in dashed lines are the effective rate
 .
The rates are normalized to liquid
hydrogen density.
.
The rates are normalized to liquid
hydrogen density.
 |




Next: Subthreshold resonances
Up: The standard Vesman model
Previous: Decay of the molecular

![[*]](foot_motif.gif) :
:
![]() not fusing but returning to the
entrance channel
not fusing but returning to the
entrance channel
![]() .
The effective formation rate is a renormalized rate taking into account the
fusion probability, as defined in Ref. [134]:
.
The effective formation rate is a renormalized rate taking into account the
fusion probability, as defined in Ref. [134]:
![[*]](foot_motif.gif) .
.
![]() and effective fusion probabilities WF for Ki=0(ortho) and Ki=1 (para) cases, calculated by Faifman et
al. [70,71,72] for a 3 K target. Also shown are
the effective rates
and effective fusion probabilities WF for Ki=0(ortho) and Ki=1 (para) cases, calculated by Faifman et
al. [70,71,72] for a 3 K target. Also shown are
the effective rates
![]() .
Note that
.
Note that
![]() less than about 107s-1 is invisible in the scale plotted.
less than about 107s-1 is invisible in the scale plotted.
