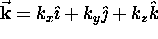 with
with
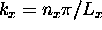 ,
,
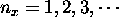 etc.
Now there is
etc.
Now there is 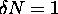 allowed
allowed
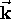 for each
``k-volume'' element
for each
``k-volume'' element 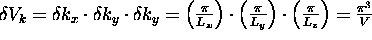 ,
where
,
where 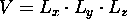 is the actual physical volume
of the three-dimensional box to which the waves are confined.
This gives a density of modes in k-space of
is the actual physical volume
of the three-dimensional box to which the waves are confined.
This gives a density of modes in k-space of
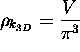 .
.
In three dimensions, the extension is straightforward:
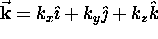 with
with
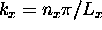 ,
,
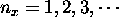 etc.
Now there is
etc.
Now there is 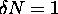 allowed
allowed
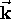 for each
``k-volume'' element
for each
``k-volume'' element 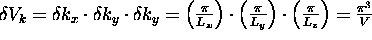 ,
where
,
where 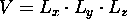 is the actual physical volume
of the three-dimensional box to which the waves are confined.
This gives a density of modes in k-space of
is the actual physical volume
of the three-dimensional box to which the waves are confined.
This gives a density of modes in k-space of
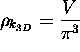 .
.
The ``volume'' of k-space having wavenumbers within
dk of  is now the positive octant
of a spherical shell of ``radius'' k
and thickness dk:
is now the positive octant
of a spherical shell of ``radius'' k
and thickness dk:
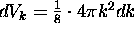 and this shell contains
and this shell contains
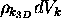 allowed modes,
so the density of wavenumber
magnitudes (distribution function) in 3D k-space is
allowed modes,
so the density of wavenumber
magnitudes (distribution function) in 3D k-space is
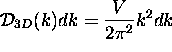 .
Note that in this case the density increases as the square
of the wavenumber. In fact, we can generalize: if d is the
dimensionality of the region of confinement, then
.
Note that in this case the density increases as the square
of the wavenumber. In fact, we can generalize: if d is the
dimensionality of the region of confinement, then
 .
In each case, the density of states in k-space is directly proportional
to the size of the real-space region to which the waves are confined.
More room, more possibilities.
.
In each case, the density of states in k-space is directly proportional
to the size of the real-space region to which the waves are confined.
More room, more possibilities.