Next: Counting Modes in 3D
Up: k-Space
Previous: Counting Modes in 1D
In a rectangular box of width 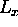 and height
and height 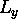 the modes which have
nodes at all boundaries are products of sinusoidal functions of the form
the modes which have
nodes at all boundaries are products of sinusoidal functions of the form
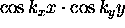 , where
, where
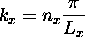 and
and
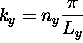 .
Now the situation is a little more complicated, since
.
Now the situation is a little more complicated, since
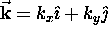 is a vector.
In fact, we call it the wavevector
instead of the wave number;
the wave number
is a vector.
In fact, we call it the wavevector
instead of the wave number;
the wave number
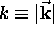 is then given by
is then given by
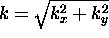 .
.
Why do we bother with the magnitude k
instead of sticking to the intrinsically multidimensional vector
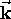 ?
Well, when we do kinematics we are often
concerned with the kinetic energy, which is a scalar
quantity depending only upon the magnitude of the momentum p
(and upon the effective mass, if any) of the particle in question.
Since we have discovered that photons (for example) are
in some sense particles which have energy
?
Well, when we do kinematics we are often
concerned with the kinetic energy, which is a scalar
quantity depending only upon the magnitude of the momentum p
(and upon the effective mass, if any) of the particle in question.
Since we have discovered that photons (for example) are
in some sense particles which have energy
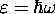 and momentum
and momentum
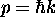 ,
we can conclude that
,
we can conclude that 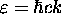 (for massless particles only)
and so, if all we really care about is the energy
(for massless particles only)
and so, if all we really care about is the energy
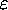 of a given mode, the only thing we need to know is its
wave number, k .
of a given mode, the only thing we need to know is its
wave number, k .
But we still need to count up how many modes have (approximately)
the same wavenumber k . This is where we have to return to the
two-dimensional picture and begin talking in terms of
k-space.
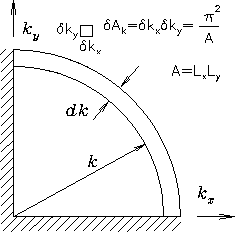
There is one allowed 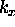 for every
for every 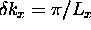 and one allowed
and one allowed 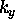 for every
for every
 , so there
is altogether
, so there
is altogether 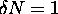 allowed
allowed
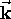 for every ``k-area'' element
for every ``k-area'' element
 in two-dimensional k-space.
(Yes, this is getting a little weird. Pay close attention!)
Note that
in two-dimensional k-space.
(Yes, this is getting a little weird. Pay close attention!)
Note that 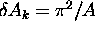 where
where
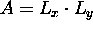 is the
actual physical area of the box in normal space.
This element of k-space contains exactly
is the
actual physical area of the box in normal space.
This element of k-space contains exactly
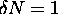 allowed state,
so once again we may define the density of states in k-space,
allowed state,
so once again we may define the density of states in k-space,
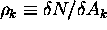 or, for this two-dimensional (2D) case,
or, for this two-dimensional (2D) case,
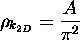 .
Note that the density of states in k-space is proportional to
the physical area of the region to which the waves are confined.
.
Note that the density of states in k-space is proportional to
the physical area of the region to which the waves are confined.
How many such states have (approximately) the same wavenumber k?
This is a crucial question in many problems.
To estimate the result we draw a ring in k-space
with radius k and width dk.
Recalling that only positive
values of 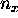 and
and
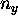 are allowed
(standing waves and all that),
we only consider the upper right-hand quadrant of the circular ring;
its ``k-area'' is thus
are allowed
(standing waves and all that),
we only consider the upper right-hand quadrant of the circular ring;
its ``k-area'' is thus 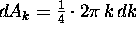 .
At a density of
.
At a density of 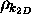 states per unit k-area, this gives
states per unit k-area, this gives
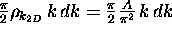 or
or  states in that ring quadrant.
We can express this as a density of wavenumber magnitudes
in terms of the distribution function
states in that ring quadrant.
We can express this as a density of wavenumber magnitudes
in terms of the distribution function
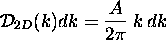 which is defined as the number of allowed modes whose wavenumbers
are within dk of a given k.
Note that the number increases linearly with k,
unlike in the 1D case where it is independent of k.
which is defined as the number of allowed modes whose wavenumbers
are within dk of a given k.
Note that the number increases linearly with k,
unlike in the 1D case where it is independent of k.
Next:
Counting Modes in 3D
Up:
k-Space
Previous:
Counting Modes in 1D
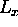 and height
and height 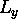 the modes which have
nodes at all boundaries are products of sinusoidal functions of the form
the modes which have
nodes at all boundaries are products of sinusoidal functions of the form
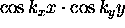 , where
, where
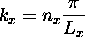 and
and
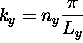 .
Now the situation is a little more complicated, since
.
Now the situation is a little more complicated, since
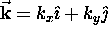 is a vector.
In fact, we call it the wavevector
instead of the wave number;
the wave number
is a vector.
In fact, we call it the wavevector
instead of the wave number;
the wave number
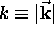 is then given by
is then given by
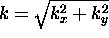 .
.
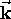 ?
Well, when we do kinematics we are often
concerned with the kinetic energy, which is a scalar
quantity depending only upon the magnitude of the momentum p
(and upon the effective mass, if any) of the particle in question.
Since we have discovered that photons (for example) are
in some sense particles which have energy
?
Well, when we do kinematics we are often
concerned with the kinetic energy, which is a scalar
quantity depending only upon the magnitude of the momentum p
(and upon the effective mass, if any) of the particle in question.
Since we have discovered that photons (for example) are
in some sense particles which have energy
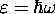 and momentum
and momentum
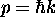 ,
we can conclude that
,
we can conclude that 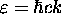 (for massless particles only)
and so, if all we really care about is the energy
(for massless particles only)
and so, if all we really care about is the energy
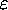 of a given mode, the only thing we need to know is its
wave number, k .
of a given mode, the only thing we need to know is its
wave number, k .
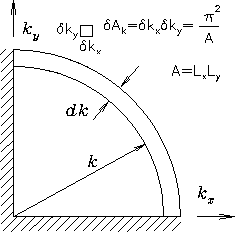
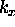 for every
for every 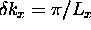 and one allowed
and one allowed 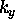 for every
for every
 , so there
is altogether
, so there
is altogether 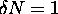 allowed
allowed
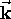 for every ``k-area'' element
for every ``k-area'' element
 in two-dimensional k-space.
(Yes, this is getting a little weird. Pay close attention!)
Note that
in two-dimensional k-space.
(Yes, this is getting a little weird. Pay close attention!)
Note that 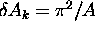 where
where
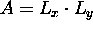 is the
actual physical area of the box in normal space.
This element of k-space contains exactly
is the
actual physical area of the box in normal space.
This element of k-space contains exactly
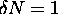 allowed state,
so once again we may define the density of states in k-space,
allowed state,
so once again we may define the density of states in k-space,
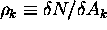 or, for this two-dimensional (2D) case,
or, for this two-dimensional (2D) case,
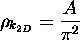 .
Note that the density of states in k-space is proportional to
the physical area of the region to which the waves are confined.
.
Note that the density of states in k-space is proportional to
the physical area of the region to which the waves are confined.
 and
and
 are allowed
(standing waves and all that),
we only consider the upper right-hand quadrant of the circular ring;
its ``k-area'' is thus
are allowed
(standing waves and all that),
we only consider the upper right-hand quadrant of the circular ring;
its ``k-area'' is thus 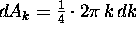 .
At a density of
.
At a density of 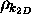 states per unit k-area, this gives
states per unit k-area, this gives
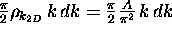 or
or  states in that ring quadrant.
We can express this as a density of wavenumber magnitudes
in terms of the distribution function
states in that ring quadrant.
We can express this as a density of wavenumber magnitudes
in terms of the distribution function
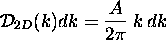 which is defined as the number of allowed modes whose wavenumbers
are within dk of a given k.
Note that the number increases linearly with k,
unlike in the 1D case where it is independent of k.
which is defined as the number of allowed modes whose wavenumbers
are within dk of a given k.
Note that the number increases linearly with k,
unlike in the 1D case where it is independent of k.