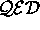 has a
strength of
has a
strength of 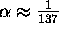 , which makes
``higher order diagrams'' rapidly insignificant --- great
for calculating with a perturbation theory!
, which makes
``higher order diagrams'' rapidly insignificant --- great
for calculating with a perturbation theory!
It didn't take long for the theory of strong interactions
to run into problems. The essence of the difficulty lies
in the very word ``strong.'' The strength of an interaction
can be calibrated by the magnitude of the dimensionless
coupling constant applied at each vertex
[wherever a virtual particle is created or annihilated]
in a Feynman diagram such as Fig. 1.
As explained earlier, each such vertex in 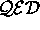 has a
strength of
has a
strength of 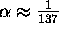 , which makes
``higher order diagrams'' rapidly insignificant --- great
for calculating with a perturbation theory!
, which makes
``higher order diagrams'' rapidly insignificant --- great
for calculating with a perturbation theory!
Unfortunately, the ``strength'' of a vertex in strong interactions
is on the order of 1. This means that the single pion exchange
diagram shown on the left in Fig. 3
or Fig. 4 is in principle no more likely
than the incomprehensible mess on the right in Fig. 4,
involving manifold exchanges of pions and other mesons, as well as
creation and annihilation of baryon-antibaryon pairs.![]() Worse yet, this is only one example of the seemingly endless
variety of possible diargams one must in principle consider in order
to make an accurate calculation of ``simple'' nucleon-nucleon scattering!
Worse yet, this is only one example of the seemingly endless
variety of possible diargams one must in principle consider in order
to make an accurate calculation of ``simple'' nucleon-nucleon scattering!

Figure:
Left: Feynman diagram for single pion exchange.
Right: A far more complicated Feynman diagram
that is in principle no less important!
Of course, it wasn't quite that bad. Handy ``sum rules''
were discovered that explained why single pion exchange usually
got you pretty close to the right answer, but in principle
one had to make an almost infinitely difficult calculation
in order to get the sort of precise predictions that
Perturbation Theorists had come to expect from their experiences
with 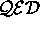 . Moreover, there were conceptual nightmares to sweat out ---
if you look closely at Fig. 4, for instance,
you will notice that a proton can emit a pion [OK, there are pions
inside protons] which can turn into a proton-antiproton pair
[OK, there are protons inside pions... Wait a minute!]
and so on. Like many nightmares, this revealed an unexplored
avenue of understanding: in the 1960's and 70's, Geoffrey Chew
and his Theory group at Berkeley developed a non-perturbative
theory of strong interactions that contained the ``bootstrap
principle:'' every hadron is made up of combinations of all
the other hadrons (and itself). Although I never could understand
Chew's models, they represented a genuinely new paradigm that
gained a good deal of purchase on the problem when suddenly
the attention of the particle physics community was diverted
by a revival of perturbation theory in the form of a quark
model, about which I will say more later; since then Chew's
approach has been sadly neglected, which I suspect is a great loss
to physics. Still, if we can get answers more easily by
``recycling an old paradigm,'' the outcome is inevitable.
. Moreover, there were conceptual nightmares to sweat out ---
if you look closely at Fig. 4, for instance,
you will notice that a proton can emit a pion [OK, there are pions
inside protons] which can turn into a proton-antiproton pair
[OK, there are protons inside pions... Wait a minute!]
and so on. Like many nightmares, this revealed an unexplored
avenue of understanding: in the 1960's and 70's, Geoffrey Chew
and his Theory group at Berkeley developed a non-perturbative
theory of strong interactions that contained the ``bootstrap
principle:'' every hadron is made up of combinations of all
the other hadrons (and itself). Although I never could understand
Chew's models, they represented a genuinely new paradigm that
gained a good deal of purchase on the problem when suddenly
the attention of the particle physics community was diverted
by a revival of perturbation theory in the form of a quark
model, about which I will say more later; since then Chew's
approach has been sadly neglected, which I suspect is a great loss
to physics. Still, if we can get answers more easily by
``recycling an old paradigm,'' the outcome is inevitable.