According to statistical theory, a measured probability distribution such as Fig. 1.1 can be approximated by a ``normal distribution function'':
where 
is the number of measurements between
x and 
, N is the total number of measurements,
is the mean and 
is the standard deviation.
The normal distribution function is plotted in
Fig. 1.2.
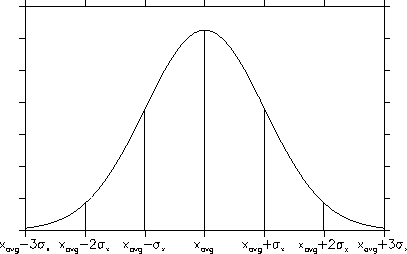
Figure 1.2:
Normal distribution function --
68% of the area under the curve lies within 
of the mean and only 5% lies more than 
away from the mean.
Note again that there are long tails, indicating that a small fraction of the
measurements will be much more than away from the mean value. For
the normal distribution, 5 % of the measurements will be more than
away from
while 68 % are within of . This well-known
distribution is also sometimes called the ``Gaussian'' distribution, or the
``Bell-curve."