BELIEVE   ME   NOT!    - -     A   SKEPTICs   GUIDE  

Time Dilation

  

Figure: A ``light clock'' is constructed aboard a glass spaceship (reference frame O') as follows: the ``tick'' of the clock is defined by one half the time interval  t'  required for the light from a strobe light to traverse the width of the ship (a height h), bounce off a mirror and come back, a total distance of 2h. In the reference frame of a ground-based observer O (with respect to whom the ship is travelling at a velocity u), the light is emitted a distance  2ut  behind the place where it is detected a time  2t  later. Since the light has further to go in the O frame (a distance $\ell = \sqrt{h^2 + u^2t^2}$), but it travels at  c  in both frames,  t  must be longer than  t'. This effect is known as TIME DILATION.

Fig. 23.3 pictures a device used by R.P. Feynman, among others, to illustrate the phenomenon of TIME DILATION: a clock aboard a fast-moving vessel (even a normal clock) appears^23.7 to run slower when observed from the ``rest frame'' -- the name we give to the reference frame arbitrarily chosen to be at rest. Now, if we choose to regard the ship's frame as ``at rest'' (as is the wont of those aboard) and the Earth as ``moving,'' a clock on Earth will appear to be running slowly when observed from the ship! Who is right? The correct answer is ``both,'' in utter disregard for common sense. This seems to create a logical paradox, which we will discuss momentarily. But first let's go beyond the qualitative statement, ``The clock runs slower,'' and ask how much slower.

For this we need only a little algebra and geometry; nevertheless, the derivation is perilous, so watch carefully. For O', the time interval described in Fig. 23.3 is simply

$$t' \; = \; {h \over c} \qquad \qquad \hbox{\rm so that} \qquad \qquad h \; = \; ct'$$

whereas for O the time interval is given by

$$t \; = \; {\ell \over c} \qquad \qquad \hbox{\rm where} \qquad \qquad \ell^2 \; = \; h^2 \; + \; u^2 t^2$$

by the Pythagorean theorem. Expanding the latter equation gives

$$t \; = \; {\sqrt{ h^2 + u^2 t^2 } \over c} \qquad \qquad \hbox{\rm or} \qquad \qquad c^2 t^2 \; = \; h^2 \; + \; u^2 t^2$$

which is not a solution yet because it does not relate  t  to  t'. We need to ``plug in''   h² = c² t'²  from earlier, to get

$$\begin{eqnarray*}c^2 t^2 &=& c^2 t'^2 \; + \; u^2 t^2 \cr \hbox{\rm or} \qquad . . . . . . , t^2 \cr \hbox{\rm or} \qquad t^2 \, (1 - \beta^2) &=& t'^2 \end{eqnarray*}$$

where we have recalled the definition   $\beta \equiv u/c$. In one last step we obtain

$$t \; = \; { t' \over \sqrt{ 1 - \beta^2 } } \qquad \qquad \hbox{\rm or} \qquad \qquad t \; = \; \gamma \; t'$$

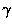where  $\gamma$  is defined as before: $\gamma \equiv 1/\sqrt{1 - \beta^2}$.

This derivation is a little crude, but it shows where 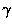 $\gamma$  comes from.