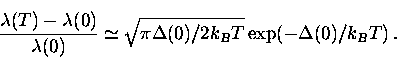Next: 2.1.3 Penetration Depth for dx-y-Wave
Up: 2.1 The Magnetic Penetration
Previous: 2.1.1 The London Penetration
Consider the BCS ground state for a
conventional superconductor with a cylindrical Fermi surface,
such that the axis of the Fermi cylinder is parallel to the
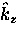 -axis.
A cross-section of the Fermi cylinder in the
-axis.
A cross-section of the Fermi cylinder in the
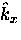 -
-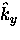 plane is
shown in Fig 2.2. In the superconducting ground state, the
electrons near the Fermi surface are paired
through a virtual phonon-induced attractive interaction
(i.e. Cooper pairs). The BCS ground state differs from the normal
state in that some of the states just above the normal Fermi surface
are occupied, while some just below are unoccupied.
The attractive interaction between paired electrons
lowers the total energy relative to the
normal ground state of unpaired electrons. The energy reduction is
maximized if the two electrons
making up a pair (i) have equal and opposite momenta
plane is
shown in Fig 2.2. In the superconducting ground state, the
electrons near the Fermi surface are paired
through a virtual phonon-induced attractive interaction
(i.e. Cooper pairs). The BCS ground state differs from the normal
state in that some of the states just above the normal Fermi surface
are occupied, while some just below are unoccupied.
The attractive interaction between paired electrons
lowers the total energy relative to the
normal ground state of unpaired electrons. The energy reduction is
maximized if the two electrons
making up a pair (i) have equal and opposite momenta 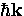 and
and
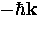 , so that the total center-of-mass momentum of
a Cooper pair is zero and (ii) if they
have opposite spins (i.e. in a spin-singlet
state
, so that the total center-of-mass momentum of
a Cooper pair is zero and (ii) if they
have opposite spins (i.e. in a spin-singlet
state 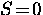 ).
The two electrons which make up a Cooper pair are continuously scattered
between states of equal and opposite momentum by virtual phonons.
However, the scattering pairs interfere with each other
so that the superconducting state is a highly correlated many-body state.
The BCS theory calculates the superconducting ground state using an explicit
N-particle wavefunction with all of these correlations built in.
The wavefunctions corresponding to the Cooper pairs in the original
BCS theory were assumed to have orbital angular momentum
).
The two electrons which make up a Cooper pair are continuously scattered
between states of equal and opposite momentum by virtual phonons.
However, the scattering pairs interfere with each other
so that the superconducting state is a highly correlated many-body state.
The BCS theory calculates the superconducting ground state using an explicit
N-particle wavefunction with all of these correlations built in.
The wavefunctions corresponding to the Cooper pairs in the original
BCS theory were assumed to have orbital angular momentum  .
Thus, in a conventional superconductor
the pairing is considered to be s-wave, spin
singlet.
At a given instant of time, a
Cooper pair is in a state
.
Thus, in a conventional superconductor
the pairing is considered to be s-wave, spin
singlet.
At a given instant of time, a
Cooper pair is in a state 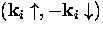 ,where the wavefunction describing the pair consists of all states
``i'' occupied by the pair during its lifetime.
It should be noted that the original BCS theory can be extended to
explain other systems.
For instance, the BCS theory can be generalized to describe
the superfluid state of 3He. The 3He
atoms form p-wave (
,where the wavefunction describing the pair consists of all states
``i'' occupied by the pair during its lifetime.
It should be noted that the original BCS theory can be extended to
explain other systems.
For instance, the BCS theory can be generalized to describe
the superfluid state of 3He. The 3He
atoms form p-wave (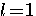 ) spin-triplet (
) spin-triplet (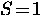 )pairs. In this case, the 3He atoms are held together by
magnetic interactions, rather than phonons.
)pairs. In this case, the 3He atoms are held together by
magnetic interactions, rather than phonons.
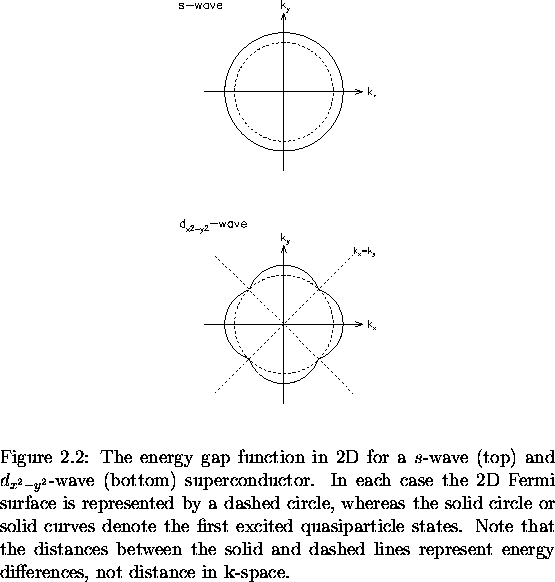
One of the important features emerging from the BCS theory, is the existence
of a temperature-dependent energy gap function 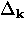 at the Fermi surface.
For an energy gap with s-wave symmetry,
at the Fermi surface.
For an energy gap with s-wave symmetry, 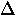 is independent
of
is independent
of 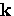 . The energy gap
. The energy gap 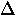 is the minimum energy required
to create a single electron (hole) excitation from the superconducting
ground state, so that the binding energy of a Cooper pair is
is the minimum energy required
to create a single electron (hole) excitation from the superconducting
ground state, so that the binding energy of a Cooper pair is  .Many conventional superconductors are in the weak-coupling limit in which
.Many conventional superconductors are in the weak-coupling limit in which
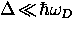 , where
, where 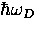 is the
Debye energy for phonons in the lattice. In the weak-coupling limit
at
is the
Debye energy for phonons in the lattice. In the weak-coupling limit
at 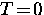 , the uniform energy gap is simply proportional to Tc
, the uniform energy gap is simply proportional to Tc
| 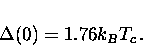 |
(22) |
At arbitrary temperature the energy gap is given by
| ![\begin{displaymath}
\Delta (T) = \Delta(0) \exp \left[ f(\Delta(T)/k_B T) \right] \, ,\end{displaymath}](img83.gif) |
(23) |
where f is a universal function of the ratio 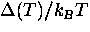 .Near Tc this yields
.Near Tc this yields
| 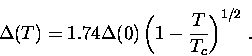 |
(24) |
As the temperature is raised above 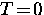 , an increasing
number of electrons are thermally excited across the energy gap
into single quasiparticle states. The minimum energy to create
an excitation is
, an increasing
number of electrons are thermally excited across the energy gap
into single quasiparticle states. The minimum energy to create
an excitation is  , which is the binding energy of a
Cooper pair. A single quasiparticle excitation of momentum
, which is the binding energy of a
Cooper pair. A single quasiparticle excitation of momentum 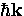 has energy
has energy
| 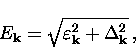 |
(25) |
where 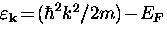 is the quasiparticle energy in the absence of a gap measured
relative to the Fermi surface.
is the quasiparticle energy in the absence of a gap measured
relative to the Fermi surface.
The penetration depth in BCS theory is determined by first calculating
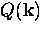 and then substituting the result into Eq. (2.5).
The expression for the BCS kernel is nonlocal, and therefore more
general than the London kernel.
Since the expression for
and then substituting the result into Eq. (2.5).
The expression for the BCS kernel is nonlocal, and therefore more
general than the London kernel.
Since the expression for 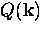 and hence
and hence
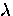 turns out to be nontrivial, only the BCS result
in the low-temperature limit is presented here. In particular,
for a clean superconductor in which
turns out to be nontrivial, only the BCS result
in the low-temperature limit is presented here. In particular,
for a clean superconductor in which 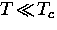 ,the number of quasiparticles excited to energy states above the gap is
exponentially activated such that [10]
,the number of quasiparticles excited to energy states above the gap is
exponentially activated such that [10]
| 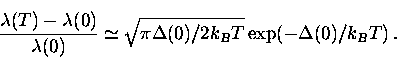 |
(26) |




Next: 2.1.3 Penetration Depth for dx-y-Wave
Up: 2.1 The Magnetic Penetration
Previous: 2.1.1 The London Penetration
![]() -axis.
A cross-section of the Fermi cylinder in the
-axis.
A cross-section of the Fermi cylinder in the
![]() -
-![]() plane is
shown in Fig 2.2. In the superconducting ground state, the
electrons near the Fermi surface are paired
through a virtual phonon-induced attractive interaction
(i.e. Cooper pairs). The BCS ground state differs from the normal
state in that some of the states just above the normal Fermi surface
are occupied, while some just below are unoccupied.
The attractive interaction between paired electrons
lowers the total energy relative to the
normal ground state of unpaired electrons. The energy reduction is
maximized if the two electrons
making up a pair (i) have equal and opposite momenta
plane is
shown in Fig 2.2. In the superconducting ground state, the
electrons near the Fermi surface are paired
through a virtual phonon-induced attractive interaction
(i.e. Cooper pairs). The BCS ground state differs from the normal
state in that some of the states just above the normal Fermi surface
are occupied, while some just below are unoccupied.
The attractive interaction between paired electrons
lowers the total energy relative to the
normal ground state of unpaired electrons. The energy reduction is
maximized if the two electrons
making up a pair (i) have equal and opposite momenta ![]() and
and
![]() , so that the total center-of-mass momentum of
a Cooper pair is zero and (ii) if they
have opposite spins (i.e. in a spin-singlet
state
, so that the total center-of-mass momentum of
a Cooper pair is zero and (ii) if they
have opposite spins (i.e. in a spin-singlet
state ![]() ).
The two electrons which make up a Cooper pair are continuously scattered
between states of equal and opposite momentum by virtual phonons.
However, the scattering pairs interfere with each other
so that the superconducting state is a highly correlated many-body state.
The BCS theory calculates the superconducting ground state using an explicit
N-particle wavefunction with all of these correlations built in.
The wavefunctions corresponding to the Cooper pairs in the original
BCS theory were assumed to have orbital angular momentum
).
The two electrons which make up a Cooper pair are continuously scattered
between states of equal and opposite momentum by virtual phonons.
However, the scattering pairs interfere with each other
so that the superconducting state is a highly correlated many-body state.
The BCS theory calculates the superconducting ground state using an explicit
N-particle wavefunction with all of these correlations built in.
The wavefunctions corresponding to the Cooper pairs in the original
BCS theory were assumed to have orbital angular momentum ![]() .
Thus, in a conventional superconductor
the pairing is considered to be s-wave, spin
singlet.
At a given instant of time, a
Cooper pair is in a state
.
Thus, in a conventional superconductor
the pairing is considered to be s-wave, spin
singlet.
At a given instant of time, a
Cooper pair is in a state ![]() ,where the wavefunction describing the pair consists of all states
``i'' occupied by the pair during its lifetime.
It should be noted that the original BCS theory can be extended to
explain other systems.
For instance, the BCS theory can be generalized to describe
the superfluid state of 3He. The 3He
atoms form p-wave (
,where the wavefunction describing the pair consists of all states
``i'' occupied by the pair during its lifetime.
It should be noted that the original BCS theory can be extended to
explain other systems.
For instance, the BCS theory can be generalized to describe
the superfluid state of 3He. The 3He
atoms form p-wave (![]() ) spin-triplet (
) spin-triplet (![]() )pairs. In this case, the 3He atoms are held together by
magnetic interactions, rather than phonons.
)pairs. In this case, the 3He atoms are held together by
magnetic interactions, rather than phonons.
![]() at the Fermi surface.
For an energy gap with s-wave symmetry,
at the Fermi surface.
For an energy gap with s-wave symmetry, ![]() is independent
of
is independent
of ![]() . The energy gap
. The energy gap ![]() is the minimum energy required
to create a single electron (hole) excitation from the superconducting
ground state, so that the binding energy of a Cooper pair is
is the minimum energy required
to create a single electron (hole) excitation from the superconducting
ground state, so that the binding energy of a Cooper pair is ![]() .Many conventional superconductors are in the weak-coupling limit in which
.Many conventional superconductors are in the weak-coupling limit in which
![]() , where
, where ![]() is the
Debye energy for phonons in the lattice. In the weak-coupling limit
at
is the
Debye energy for phonons in the lattice. In the weak-coupling limit
at ![]() , the uniform energy gap is simply proportional to Tc
, the uniform energy gap is simply proportional to Tc
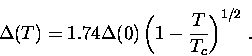
![]() and then substituting the result into Eq. (2.5).
The expression for the BCS kernel is nonlocal, and therefore more
general than the London kernel.
Since the expression for
and then substituting the result into Eq. (2.5).
The expression for the BCS kernel is nonlocal, and therefore more
general than the London kernel.
Since the expression for ![]() and hence
and hence
![]() turns out to be nontrivial, only the BCS result
in the low-temperature limit is presented here. In particular,
for a clean superconductor in which
turns out to be nontrivial, only the BCS result
in the low-temperature limit is presented here. In particular,
for a clean superconductor in which ![]() ,the number of quasiparticles excited to energy states above the gap is
exponentially activated such that [10]
,the number of quasiparticles excited to energy states above the gap is
exponentially activated such that [10]