


Next: 3.2.5 The Fourier Transform
Up: 3.2 Measuring the Internal
Previous: 3.2.3 The Relaxation Function
Now consider the complete set of four positron counters in Fig. 3.1.
Ignoring geometric misalignments and differences in counter efficiency,
the x-component of the muon polarization Px(t)
[monitored by the L and R counters]
differs from the y-component of the muon polarization Py(t)
[monitored by the U and D counters] by a phase of 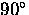 .
The two components of the muon polarization can be combined to form a
``complex'' polarization function
.
The two components of the muon polarization can be combined to form a
``complex'' polarization function
| 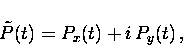 |
(25) |
where
| 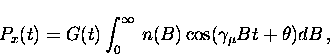 |
(26) |
and
The complex asymmetry for the four-counter setup is defined as
where Ax(t) and Ay(t) are the real and imaginary
parts of the complex asymmetry, respectively. The number of counts
per second in the ith counter (i = L, R, U or D) is
| ![\begin{displaymath}
N_{i}(t) = N_{i}^{\circ} e^{-t/ \tau_{\mu}} \left[ 1 + A_{i}(t)
\right] + B_{i} \, ,\end{displaymath}](img270.gif) |
(27) |
where 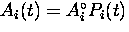 is the asymmetry function
for the ith raw histogram. Rearranging Eq. (3.29)
gives
is the asymmetry function
for the ith raw histogram. Rearranging Eq. (3.29)
gives
| ![\begin{displaymath}
A_{i}(t) = e^{t/ \tau_{\mu}} \left[
\frac{N_{i}(t) - B_{i}}{N_{i}^{\circ}} \right] - 1 \, .\end{displaymath}](img272.gif) |
(28) |
In terms of the individual counters, the real asymmetry
Ax(t) and the imaginary asymmetry Ay(t) are
In this thesis the real and imaginary parts of the asymmetry were
fit simultaneously, assuming a phase difference of 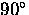 between
them.
between
them.



Next: 3.2.5 The Fourier Transform
Up: 3.2 Measuring the Internal
Previous: 3.2.3 The Relaxation Function
![]() .
The two components of the muon polarization can be combined to form a
``complex'' polarization function
.
The two components of the muon polarization can be combined to form a
``complex'' polarization function
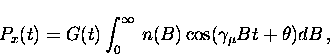
![\begin{displaymath}
A_{i}(t) = e^{t/ \tau_{\mu}} \left[
\frac{N_{i}(t) - B_{i}}{N_{i}^{\circ}} \right] - 1 \, .\end{displaymath}](img272.gif)