


Next: The Coherence Length (Pippard's Equation)
Up: Magnetic Properties of Conventional Superconductors
Previous: Type-I Superconductors
In 1935, F. and H. London modified an essential equation of electrodynamics
(i.e. Ohm's Law) in such a way as to obtain the Meissner effect, without
altering Maxwell's equations themselves. In doing so, they incorporated the
two-fluid model of Gorter and Casimir [12]. The two-fluid model
separates the electron system into a superconducting component with an
electron density ns, and a normal component with an electron density
nn. They assumed the total electron density
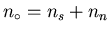 behaved such that
behaved such that
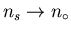 as
as
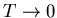 ,
and
,
and
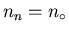 when T > Tc.
Emerging from their phenomenological model
is the so-called
London penetration depth
when T > Tc.
Emerging from their phenomenological model
is the so-called
London penetration depth
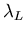 [13]:
[13]:
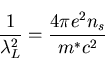 |
(1) |
where m* is the effective mass of the superconducting carriers, and
ns is the superconductor carrier density.
Pure-elemental metals and
low concentration alloys
(eg. dilute SnIn alloy system [14]),
where
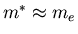 (free electron mass),
tend to be type-I. Generally speaking,
(free electron mass),
tend to be type-I. Generally speaking,
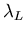 is short and the Fermi
velocity of the superconducting carriers
vF is high in these materials [15].
is short and the Fermi
velocity of the superconducting carriers
vF is high in these materials [15].
The physical significance of
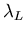 pertains to the failure of the
Meissner effect to occur abruptly at the surface of a superconductor;
rather the magnetic field penetrates slightly into the bulk of the
superconducting material
on a length scale given by
pertains to the failure of the
Meissner effect to occur abruptly at the surface of a superconductor;
rather the magnetic field penetrates slightly into the bulk of the
superconducting material
on a length scale given by
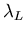 .
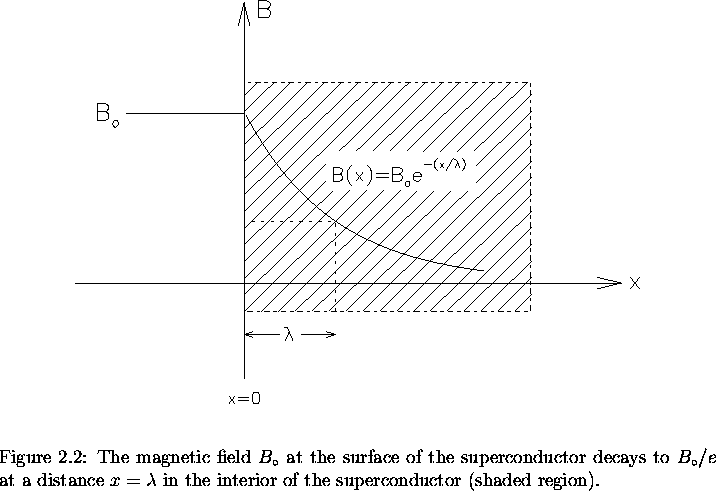
Consider a semi-infinite superconductor with the boundary between
normal and superconducting regions at x=0. In the presence of an
external magnetic field applied perpendicular to the surface,
London theory predicts
that the magnetic flux decays exponentially
into the bulk of the superconductor according to
[13,16]:
.
Consider a semi-infinite superconductor with the boundary between
normal and superconducting regions at x=0. In the presence of an
external magnetic field applied perpendicular to the surface,
London theory predicts
that the magnetic flux decays exponentially
into the bulk of the superconductor according to
[13,16]:
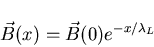 |
(2) |
where 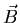 (0) is the magnetic field at the surface of
the superconductor, and x is the distance into the superconductor
from the surface (see Fig. 2.2). The expulsion of the magnetic
field is accomplished by shielding currents (or supercurrents)
which flow at the
surface of the superconductor without any Ohmic losses.
These supercurrents
form a finite sheath which is spread out to a thickness
(0) is the magnetic field at the surface of
the superconductor, and x is the distance into the superconductor
from the surface (see Fig. 2.2). The expulsion of the magnetic
field is accomplished by shielding currents (or supercurrents)
which flow at the
surface of the superconductor without any Ohmic losses.
These supercurrents
form a finite sheath which is spread out to a thickness
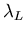 into the sample. Such a distribution of current is much more
energetically favourable than an infinitely thin sheath of current
[13].
The supercurrent density
into the sample. Such a distribution of current is much more
energetically favourable than an infinitely thin sheath of current
[13].
The supercurrent density
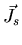 is related to the local magnetic
flux density
is related to the local magnetic
flux density 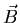 by Ampére's Law:
by Ampére's Law:
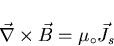 |
(3) |



Next: The Coherence Length (Pippard's Equation)
Up: Magnetic Properties of Conventional Superconductors
Previous: Type-I Superconductors
Jess H. Brewer
2001-09-28
![]() behaved such that
behaved such that
![]() as
as
![]() ,
and
,
and
![]() when T > Tc.
Emerging from their phenomenological model
is the so-called
London penetration depth
when T > Tc.
Emerging from their phenomenological model
is the so-called
London penetration depth
![]() [13]:
[13]:
![]() pertains to the failure of the
Meissner effect to occur abruptly at the surface of a superconductor;
rather the magnetic field penetrates slightly into the bulk of the
superconducting material
on a length scale given by
pertains to the failure of the
Meissner effect to occur abruptly at the surface of a superconductor;
rather the magnetic field penetrates slightly into the bulk of the
superconducting material
on a length scale given by
![]() .
Consider a semi-infinite superconductor with the boundary between
normal and superconducting regions at x=0. In the presence of an
external magnetic field applied perpendicular to the surface,
London theory predicts
that the magnetic flux decays exponentially
into the bulk of the superconductor according to
[13,16]:
.
Consider a semi-infinite superconductor with the boundary between
normal and superconducting regions at x=0. In the presence of an
external magnetic field applied perpendicular to the surface,
London theory predicts
that the magnetic flux decays exponentially
into the bulk of the superconductor according to
[13,16]: