


Next: B Numerical Integration of
Up: A Muonium Spin Polarization
Previous: A.1 Transverse Field
In the other case of interest the initial muon polarization
is along the magnetic field direction. We are then
interested in the time dependence of the
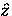 component of the muon's spin in
longitudinal field (LF).
Since muons are produced (usually) from the decay of a charged pion
(essentially at rest near the surface of the pion production target)
into a two body final state via
component of the muon's spin in
longitudinal field (LF).
Since muons are produced (usually) from the decay of a charged pion
(essentially at rest near the surface of the pion production target)
into a two body final state via
| 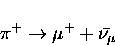 |
(20) |
and since neutrinos always have negative helicity, the muon beam
produced also has negative helicity. The initial polarization
of the muon, having stopped in a sample, is therefore in the 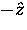 direction.
Again, muonium is formed with an electron captured from the
medium with equal probablity of having spin ``up'' or ``down''
with respect to the quantization axis.
We are interested in the matrix elements
direction.
Again, muonium is formed with an electron captured from the
medium with equal probablity of having spin ``up'' or ``down''
with respect to the quantization axis.
We are interested in the matrix elements
| 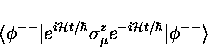 |
(21) |
and
|  |
(22) |
The first muonium state is an eigenfunction of the
Hamiltonian and the matrix element given by Eq. (A.48)
is therefore simply
|  |
(23) |
Equation (A.49) can be written
| 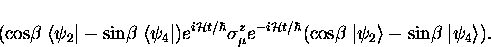 |
(24) |
Thus, using Eq. (A.17) once again,
| 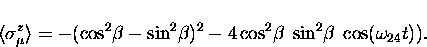 |
(25) |
Noting that
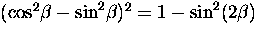 and that
and that
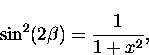
thjis can be written
| 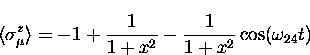 |
(26) |
where 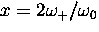 .
.
The total muon polarization 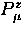 in longitudinal
field is then the sum of these two parts,
with muonium formed with equal probability in each state, giving
in longitudinal
field is then the sum of these two parts,
with muonium formed with equal probability in each state, giving
The frequency 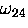 in Eq. (A.54) is sufficiently
high that in most experimental situations, at this time,
it is not directly
observable in the data as an oscillatory signal, so this term
is effectively averaged to zero by the timing resolution
of the spectrometer.
in Eq. (A.54) is sufficiently
high that in most experimental situations, at this time,
it is not directly
observable in the data as an oscillatory signal, so this term
is effectively averaged to zero by the timing resolution
of the spectrometer.
Thoughout this calculation we have not considered any
relaxation of the muonium spin polarization.



Next: B Numerical Integration of
Up: A Muonium Spin Polarization
Previous: A.1 Transverse Field
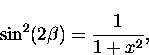
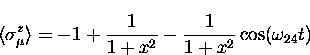
![]() in longitudinal
field is then the sum of these two parts,
with muonium formed with equal probability in each state, giving
in longitudinal
field is then the sum of these two parts,
with muonium formed with equal probability in each state, giving
![]() in Eq. (A.54) is sufficiently
high that in most experimental situations, at this time,
it is not directly
observable in the data as an oscillatory signal, so this term
is effectively averaged to zero by the timing resolution
of the spectrometer.
in Eq. (A.54) is sufficiently
high that in most experimental situations, at this time,
it is not directly
observable in the data as an oscillatory signal, so this term
is effectively averaged to zero by the timing resolution
of the spectrometer.