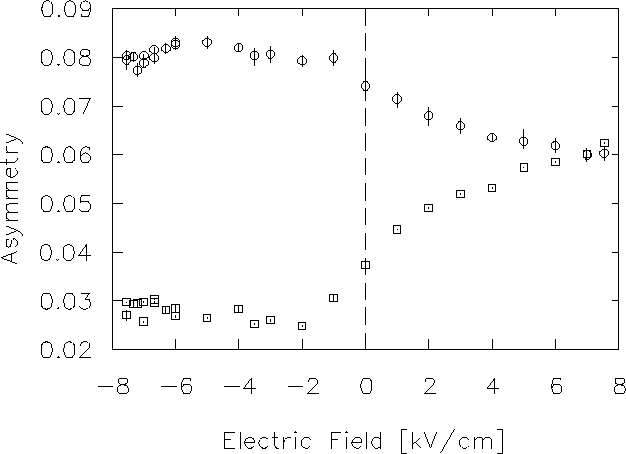
The results unambiguously indicate directional
asymmetry in the effect of an electric field.
With ![]() in the
in the ![]() direction
the muon fraction was increased and muonium decreased.
With the direction of the electric field reversed,
the asymmetries change in the opposite way.
This is consistent with a mechanism for muonium formation
in which free electrons generated in the muon's radiolysis track
neutralize the positive muon.
Applying an external electric field drives these electrons
either toward or away from the stopped muon, increasing or decreasing
the likelihood of muonium formation by putting more or fewer
electrons in the vicinity of the thermal muon.
Muonium formation in this way is always exothermic and
therefore can proceed after the muon has come to thermal energies.
Assuming this model, we can conclude that the electrons
originate predominantly behind the muon.
This model implies that the muon stops downstream from
the end of its ionization track, more or less preserving
its direction of travel while slowing down.
direction
the muon fraction was increased and muonium decreased.
With the direction of the electric field reversed,
the asymmetries change in the opposite way.
This is consistent with a mechanism for muonium formation
in which free electrons generated in the muon's radiolysis track
neutralize the positive muon.
Applying an external electric field drives these electrons
either toward or away from the stopped muon, increasing or decreasing
the likelihood of muonium formation by putting more or fewer
electrons in the vicinity of the thermal muon.
Muonium formation in this way is always exothermic and
therefore can proceed after the muon has come to thermal energies.
Assuming this model, we can conclude that the electrons
originate predominantly behind the muon.
This model implies that the muon stops downstream from
the end of its ionization track, more or less preserving
its direction of travel while slowing down.
In order for the external field to have much effect on the trajectory of electrons in the Coulomb fields of nearby ions and the muon, the electron that eventually reaches the muon must be far enough away from them, at least for part of the time-of-flight, One way for this to happen may result from the end of the cyclic charge exchange part of the muon track. A hot muonium atom can undergo a collision with a neutral atom and ionize itself, leaving the electron in the lattice while the bare muon can continue on with the last few eV and eventually come to rest further down stream. In this picture neither the electron or muon are in the immediate vicinity of any other ion. Most importantly, this electron that has been carried in a muonium atom away from the ion from which it came is the closest one to the muon and therefore is the electron that reaches the thermal muon first. This model implies that the direction of travel of the muon, at the very end of the track, is still on average in the direction of the muon beam.
 |
In order for an external electric field to have an
appreciable effect on the motion of electrons in the vicinity
of the muon, the magnitude of the external electric field would
have to be comparable to (or larger than) the electric
field due to the muon's charge.
One can then estimate the typical initial distance between
the electron and muon from the electric field dependence
of the asymmetries.
An electric field of about 3 kv/cm falls midway on the
curve between E=0 and saturation of the effect.
Taking the electric field of the muon at the electron to be
E0=3.0 kV/cm, one may conclude that the typical
electron-muon distance is approximately
![]() = 60 nm,
in which
= 60 nm,
in which ![]() is the dielectric constant
of solid nitrogen.
is the dielectric constant
of solid nitrogen.