A.2 The 10/3 effect [#!AndersonRMP53!#,#!KuboTomitaJPSJ54!#]

 This section considers nuclear spin relaxation in a paramagnetic localized spin system, with the interaction between the moments described by the dipolar fields.

We assume the Hamiltonian of the spin system to be:

where, H₀ is the external magnetic field applied in the z-direction, ${\mbox{\boldmath$S$\unboldmath}}_i$ is the spin of the i-th localized electron and D_ij represents the tensor for the dipolar interaction, namely,

where, ${\mbox{\boldmath$r$\unboldmath}}_{ij}={\mbox{\boldmath$r$\unboldmath}}_{j}-{\mbox{\boldmath$r$\unboldmath}}_i$ is the distance between the i-th and the j-th electrons and $\hat{{\mbox{\boldmath$r$\unboldmath}}}_{ij}={\mbox{\boldmath$r$\unboldmath}}_{ij}/\vert{\mbox{\boldmath$r$\unboldmath}}_{ij}\vert$ is the unit vector parallel to the distance.

It is easily shown that the fluctuation rate (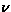$\nu$) of the electron moments doesn't depend on the external field; if one writes the Hamiltonian (eq.68) in the rotating reference frame (RRF) for the electrons, one can eliminate the external field, while the dipolar interaction is expressed as:

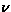where ${\cal H}_0$ is the first term of the Hamiltonian (eq.68) and ${\mbox{\boldmath$S$\unboldmath}}_{i;R}$ the RRF representation of the spin ${\mbox{\boldmath$S$\unboldmath}}_i$. This result indicates that the dipolar interaction between the electrons (namely the associated fluctuation rate $\nu$) doesn't change in RRF, because the interacting two spins ${\mbox{\boldmath$S$\unboldmath}}_j$ and ${\mbox{\boldmath$S$\unboldmath}}_i$ have the same gyromagnetic ratio, and conduct coherent precession in the external field H₀.

To the probe nuclear spin, the Larmor precession of the electron moment in a reasonably large external field H₀ is so fast that its xy components becomes invisible (Fig.64). In this limit, the probe spin detects only the z-component of the electron moments, which changes its length with the dipolar fluctuation rate (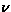$\nu$). In this situation, the T₁ relaxation rate of the probe spin may be reduced by $\sim 1/3$ from that in the zero-field case, because the average size of the z-component squared is 1/3 of the full spin: $<(S^z)^2\gt=1/3\,S^2$. As shown below, the precise factor is 3/10.

  

Figure 64: An electron moment and a muon spin in an external magnetic field (H₀). If the Larmor precession of the electron is fast, muon detects only the z-component of the electron spin S_i^z.

Generally, the T₁ relaxation rate of a probe nuclear spin is expressed as [34]:

where, $\omega_\mu$ is the Larmor precession frequency of the nuclear spin (muon), $H^a_\mu(t)$ (a=x,y) is the x,y-component of the fluctuating local fields at the probe spin site and $H^{\pm}_\mu\equiv H^{x}_\mu\pm iH^{y}_\mu$. The bracket $<\cdot\cdot\cdot\gt$ denotes the ensemble average. If the muon-electron interaction is the dipolar fields, the local field at the muon site becomes:

where ${\mbox{\boldmath$r$\unboldmath}}_j$ is the distance between the muon and the j-th electron and $\hat{\mbox{\boldmath$r$\unboldmath}}_j$ is the unit vector parallel to the distance.

To write 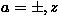$H^\pm_\mu(t)$, it is convenient to define $\hat{r}^\pm_j\equiv \hat{r}^x_j\pm i \hat{r}^y_j$, where, $\hat{r}^a_j$ (a=x,y) is the x,y-component of the unit vector $\hat{\mbox{\boldmath$r$\unboldmath}}_j$. The local fields are expressed as:

Using the rotating reference frame (RRF) for the electrons, the electron spin correlations <S^a_j(0)S^b_k(t)> ($a,b=\pm,z$) are expressed as:

where $\omega_0$ is the electron Larmor frequency, S^a_j;R(t) ($a=\pm,z$) is the electron spins expressed in the RRF. Assuming a Markoffian fluctuation processes, decay of the spin correlation is expressed as

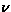where $\nu$ is the dipolar fluctuation rate, and $a,b=\pm,z$. In paramagnetic state, there is no correlation between the j-th and the k-th spin, yielding the t=0 correlation functions as:

Using the above presented expressions, the field correlation at the probe spin site becomes:

In the same manner, $<H^-_\mu(0)H^+_\mu(t)\gt$ is calculated, yielding the T₁ relaxation rate as:

In an isotropic sample, the coefficients are replaced by the angular averages:

Introducing the dipolar field width (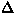$\Delta$) defined in eq.45, the T₁ relaxation yields:

Namely, if the Larmor precession of the electron moments are fast, the local field width at the muon site is effectively reduced to $\Delta^{\rm LF}=\sqrt{3/10}\,\Delta^{\rm ZF}$.