



Next: 6.1.2 Organic spin Peierls
Up: 6.1 Introduction
Previous: 6.1 Introduction
The spin-Peierls transition, which was proposed for an
antiferromagnetic S=1/2 spin chain
[14,15,16], is characterized by two
features: (1) alternating deformation of the lattice along the chain
direction, and (2) singlet pair formations of the two S=1/2 spins on
the shortened link (Fig.49b). Although the
lattice dimerization (1) increases the elastic energy, the
transition may still be possible if the singlet pair formation
(2) compensates the energy increase. In order to estimate the conditions
for spin Peierls transition, a quantum mechanical treatment of the
spin system is necessary, because singlet-pair formations
are involved in the transition mechanism.
Figure 49:
(a) An S=1/2 spin chain with a uniform antiferromagnetic interaction J.
(b) The lattice dimerized state below the spin Peierls transition temperature 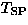 .
.
 |
A Hamiltonian of a one-dimensional spin chain which allows lattice
deformation can be expressed as:
where  is the antiferromagnetic interaction between the
spins on the i-th and the
is the antiferromagnetic interaction between the
spins on the i-th and the  -th site, K is the spring constant of
the lattice, and ui is the displacement of the lattice point i.
The first term of this Hamiltonian describes the spin system and the
second term, the elastic energy of the lattice system. Under a
lattice deformation along the chain, the antiferromagnetic coupling
-th site, K is the spring constant of
the lattice, and ui is the displacement of the lattice point i.
The first term of this Hamiltonian describes the spin system and the
second term, the elastic energy of the lattice system. Under a
lattice deformation along the chain, the antiferromagnetic coupling  is
expanded as
is
expanded as
where 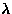 is a spin-lattice coupling constant and a is the
lattice spacing. The last equation holds for the lattice dimerized state
(displacement u) with
is a spin-lattice coupling constant and a is the
lattice spacing. The last equation holds for the lattice dimerized state
(displacement u) with  . Using eq.48
the Hamiltonian (eq.47) is rewritten as:
. Using eq.48
the Hamiltonian (eq.47) is rewritten as:
where, the second term gives a spin-lattice coupling.
Analytical approaches to the spin Peierls problem have been unsuccessful;
one popular way to solve the problem is as follows:
- (1)
- map the spin Hamiltonian to a fermion system using the
Jordan-Wigner transformation [118]
- (2)
- solve the fermion system, using various approximation
techniques developed for fermion systems
- (3)
- obtain the phonon features, with perturbation treatments of the
fermion-phonon coupling, which arose from the
spin-lattice coupling (the second term of eq.49).
Since step (2) involves the quantum mechanics of the spin system, this part is
the most crucial to this theoretical approach; indeed, the
spin-Peierls transition temperature strongly depends on this part.
Bulaevskii [119] and Pytte [120] adopted
the Hartree approximation for step (2) and calculated the phonon frequency
( ) above the spin Peierls transition temperature. Their result is:
) above the spin Peierls transition temperature. Their result is:
where,  is the bare phonon frequency,
is the bare phonon frequency,  is a dimensionless spin-lattice coupling parameter and the constants
are
is a dimensionless spin-lattice coupling parameter and the constants
are  and
and  . A softening of phonons is
predicted, as the result of fermion-phonon coupling.
From the temperature which gives a zero phonon frequency,
the spin Peierls transition temperature
. A softening of phonons is
predicted, as the result of fermion-phonon coupling.
From the temperature which gives a zero phonon frequency,
the spin Peierls transition temperature 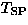 has been estimated as:
has been estimated as:
Since the Hartree approximation drops the exchange interaction between
two fermions, it may not adequately include quantum fluctuations.
In fact, a quantum mechanical treatment introduced below gives an
enhanced spin Peierls transition temperature.
Cross and Fisher
[121] approximated the mapped fermion system with an
exactly soluble model (Tomonaga-Luttinger model
[122,123]), preserving the physical
features around the Fermi surface. This approximation, which was first
introduced by Luther and Peschel [124], well describes the
low temperature behavior of the original fermion system, because
that behavior is determined by features around the Fermi surface.
Since the treatment after the approximation is exact, quantum mechanical
effects should be included correctly in the results. Cross and Fisher obtained the
phonon frequency above 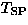 as:
as:
which gives the spin Peierls transition temperature as:
Cross and Fisher's 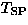 is higher than that from the Hartree
approximation (eq.51); the spin Peierls state is preferred
in a more quantum mechanical treatment. This behavior is opposite to
that of Néel temperature which usually decreases with more quantum
mechanical treatments. The difference probably originates from the
classical nature of the Néel state and the quantum mechanical singlet
nature of the spin Peierls ground state.
is higher than that from the Hartree
approximation (eq.51); the spin Peierls state is preferred
in a more quantum mechanical treatment. This behavior is opposite to
that of Néel temperature which usually decreases with more quantum
mechanical treatments. The difference probably originates from the
classical nature of the Néel state and the quantum mechanical singlet
nature of the spin Peierls ground state.
In 1980, Nakano and Fukuyama [125,126] formulated
Cross and Fisher's approach using a phase variable:
where x is the position on the chain,  is the phase
variable and p(x) is its momentum;
is the phase
variable and p(x) is its momentum;  and p(x) satisfy the
canonical relation:
and p(x) satisfy the
canonical relation:
For a dimerized Heisenberg chain, the coefficients take the following values:
|  |
(7) |
Using the phase variable  , the z-component of a spin is expressed as:
, the z-component of a spin is expressed as:
As shown in eq.57, the Néel state [ ] and
the singlet state [
] and
the singlet state [ ] are both expressed equally
in this `phase Hamiltonian' (eq.54). It has been
shown that this formalism gives the same result as Cross and
Fisher's approach, but more easily and intuitively
[125,126]. Using the phase Hamiltonian
approach, the effects of inter-chain interactions (J') and external magnetic
field (H) have been investigated [17,18].
The results are summarized as follows:
] are both expressed equally
in this `phase Hamiltonian' (eq.54). It has been
shown that this formalism gives the same result as Cross and
Fisher's approach, but more easily and intuitively
[125,126]. Using the phase Hamiltonian
approach, the effects of inter-chain interactions (J') and external magnetic
field (H) have been investigated [17,18].
The results are summarized as follows:
- (1)
- In zero-field, the ground state is either the Néel state
or spin-Peierls state, depending on the magnitude of the inter-chain
interaction. The phase boundary
 is first order, where
is first order, where  is a normalized inter-chain
interaction,
is a normalized inter-chain
interaction,  is a dimensionless spin-lattice
coupling parameter and
is a dimensionless spin-lattice
coupling parameter and  .
. - (2)
- The ground state in finite magnetic field was
obtained, as shown in Fig.50. The spin-Peierls
phase (SP) makes a first order transition to a magnetic phase
(M
 ) at a critical field (ht1). There is a spin-flop phase
(SF) in the large j' region, but experimentally the SP
) at a critical field (ht1). There is a spin-flop phase
(SF) in the large j' region, but experimentally the SP SF transition may be
difficult to observe, because of the narrow parameter range (B on the
SF transition may be
difficult to observe, because of the narrow parameter range (B on the  -axis)
as the condition.
-axis)
as the condition.
Figure:
Theoretical ground state phase diagram in magnetic field. The spin-Peierls phase
makes a first order transition to a magnetic phase (M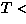 ). Cite
from Ref. [18]
). Cite
from Ref. [18]
 |




Next: 6.1.2 Organic spin Peierls
Up: 6.1 Introduction
Previous: 6.1 Introduction


![]() ) above the spin Peierls transition temperature. Their result is:
) above the spin Peierls transition temperature. Their result is:
![]() as:
as:
 is a dimensionless spin-lattice
coupling parameter and
is a dimensionless spin-lattice
coupling parameter and  -axis)
as the condition.
-axis)
as the condition.