



Next: Muon transfer
Up: Muonic atom collisions
Previous: Muonic atom collisions
Elastic scattering processes dictate the deceleration of muonic atoms in
the target, hence they determine the energy distribution at the time of the
subsequent reaction (such as muon transfer or molecular formation) in the
 CF cycle.
CF cycle.
There is a relatively limited amount of experimental information on muonic
atom scattering cross sections [24]. In particular, there is
hardly any data on energy dependent cross sections.
The elastic scattering cross section can be written in terms of the sum
of the contributions of the partial waves:
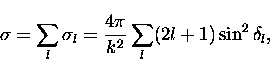 |
(1) |
where the physics is contained in the phase shift
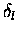 .
As one can see from Eq. 1.1, if for a given partial
wave l,
.
As one can see from Eq. 1.1, if for a given partial
wave l,
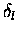 is approximately equal to
is approximately equal to 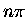 (
(
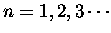 ), then
the partial cross section
), then
the partial cross section
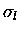 goes to zero. For low energy
collisions, where s wave (l=0) usually dominates, the total cross
section can become very small, a process known as the Ramsauer-Townsend
effect. If, on the other hand,
goes to zero. For low energy
collisions, where s wave (l=0) usually dominates, the total cross
section can become very small, a process known as the Ramsauer-Townsend
effect. If, on the other hand,
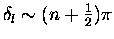 ,
then the cross section becomes large and reaches a maximum value (
,
then the cross section becomes large and reaches a maximum value (
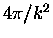 )
called the unitarity limit. It is interesting to note that all the
phase shifts at the zero energy limit are fixed at
)
called the unitarity limit. It is interesting to note that all the
phase shifts at the zero energy limit are fixed at
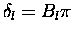 by Levinson's theorem [25,26], where Bl is the number of
three-body bound states of given l, illustrating the intricate
connection between bound states and scattering properties. As we shall see
it is the Ramsauser-Townsend effect that makes it possible to produce a
muonic atom beam for our experiments.
by Levinson's theorem [25,26], where Bl is the number of
three-body bound states of given l, illustrating the intricate
connection between bound states and scattering properties. As we shall see
it is the Ramsauser-Townsend effect that makes it possible to produce a
muonic atom beam for our experiments.




Next: Muon transfer
Up: Muonic atom collisions
Previous: Muonic atom collisions
![]() CF cycle.
CF cycle.