In this chapter, recent ![]() SR measurements of the
SR measurements of the
![]() -
-![]() plane magnetic penetration depth
plane magnetic penetration depth ![]() and the vortex core radius r0 in the conventional
type-II superconductor NbSe2
are presented.
and the vortex core radius r0 in the conventional
type-II superconductor NbSe2
are presented.
Figures 6.1 and 6.2 show
the Fourier transforms of the muon precession
signal in NbSe2 as functions of temperature and applied magnetic
field, respectively.
The horizontal axes are in terms of the internal
magnetic field B relative to the average field of the background
signal ![]() , which by definition is centered at 0 G. As the temperature
or magnetic field is lowered, the line shape broadens and the high-field
tail becomes longer due mainly to a decrease
in
, which by definition is centered at 0 G. As the temperature
or magnetic field is lowered, the line shape broadens and the high-field
tail becomes longer due mainly to a decrease
in ![]() . The high-field cutoff is clearly visible in all of the
measured line shapes for NbSe2. This implies that the vortex cores
occupy a significant volume of the sample. This fractional volume
depends on both the size of the vortex cores and the areal density
of vortices.
. The high-field cutoff is clearly visible in all of the
measured line shapes for NbSe2. This implies that the vortex cores
occupy a significant volume of the sample. This fractional volume
depends on both the size of the vortex cores and the areal density
of vortices.
In order to test the effects of the analysis procedure on the determined
behaviour of ![]() and
and ![]() , three different
models for the theoretical internal field distribution corresponding
to the vortex lattice were considered:
, three different
models for the theoretical internal field distribution corresponding
to the vortex lattice were considered:
Figure 6.3 shows the magnetic field dependence of ![]() at
at ![]() (i.e.
(i.e. ![]() K)
obtained by fitting the
K)
obtained by fitting the ![]() SR time spectra with a polarization function
which assumes one of the three models for the field distribution due
to the vortex lattice.
From magnetization measurements,
SR time spectra with a polarization function
which assumes one of the three models for the field distribution due
to the vortex lattice.
From magnetization measurements, ![]() T, so that
the results extend over the field range
T, so that
the results extend over the field range ![]() ,where
,where ![]() . A clear linear H-dependence for
. A clear linear H-dependence for
![]() is obtained for
all three types of analysis, although there is some difference in the
absolute value of
is obtained for
all three types of analysis, although there is some difference in the
absolute value of ![]() and the strength of the linear
term. The solid lines in Fig. 6.3 are fits to the linear relation
and the strength of the linear
term. The solid lines in Fig. 6.3 are fits to the linear relation
| |
(1) |
| Model for |
||
|---|---|---|
| ML: Gaussian Cutoff | 1659(1) | 1.85(4) |
| ML: Lorentzian Cutoff | 1398(2) | 0.81(3) |
| Analytical GL Model | 1323(2) | 1.62(3) |
Figure 6.4 shows the magnetic field dependence of
the quality of the fits at ![]() , obtained
for the three different models. The ratio of
, obtained
for the three different models. The ratio of ![]() to the number of degrees of freedom (NDF) is significantly
greater than 1.0 in most cases due to the high statistics
of the measured magnetic field distribution.
For a non-perfect fit, higher statistics magnify the value of
to the number of degrees of freedom (NDF) is significantly
greater than 1.0 in most cases due to the high statistics
of the measured magnetic field distribution.
For a non-perfect fit, higher statistics magnify the value of ![]() .Fits to the ML model with a
Gaussian cutoff generally yield the worst
.Fits to the ML model with a
Gaussian cutoff generally yield the worst ![]() value.
On the other hand, fits
assuming a Lorentzian cutoff are only slightly better than
fits to the analytical GL model.
value.
On the other hand, fits
assuming a Lorentzian cutoff are only slightly better than
fits to the analytical GL model.
Figure 6.5 shows, in the frequency domain, how the quality of the
fits obtained (in the time domain) from the ML model using a
Gaussian cutoff factor and from the analytical GL model are virtually
indistinguishable. One would expect the results from these two models
to converge at higher magnetic fields. However, as shown
in Fig. 6.3,
![]() determined for the two different models appear
to diverge slowly at high H.
The reason is that the analytical GL model deviates significantly
from the exact numerical GL solutions at high reduced
fields [121], and also, according to Brandt [123],
the ML model is really only applicable when
determined for the two different models appear
to diverge slowly at high H.
The reason is that the analytical GL model deviates significantly
from the exact numerical GL solutions at high reduced
fields [121], and also, according to Brandt [123],
the ML model is really only applicable when ![]() .
.
Despite the quantitative differences between the three
phenomenological models, which is related to their validity in
different field ranges, the finding of a linear-H dependence for
![]() is common to all.
Since the analytical GL model properly accounts for the finite size of the
vortex cores and our measurements are taken essentially at low
reduced fields (especially in the case of YBa2Cu3O
is common to all.
Since the analytical GL model properly accounts for the finite size of the
vortex cores and our measurements are taken essentially at low
reduced fields (especially in the case of YBa2Cu3O![]() which
we consider later) the results obtained using this model should
most faithfully reflect the behaviour of the fundamental length scales.
Unless otherwise stated, results presented in the remainder of
this thesis were obtained assuming this model.
which
we consider later) the results obtained using this model should
most faithfully reflect the behaviour of the fundamental length scales.
Unless otherwise stated, results presented in the remainder of
this thesis were obtained assuming this model.
Figure 6.6 shows a comparison between ![]() in NbSe2
at two different temperatures. A linear-H dependence is observed
between
in NbSe2
at two different temperatures. A linear-H dependence is observed
between ![]() and 0.6 Tc.
The field dependence at lower T was not investigated because
the 4He gas flow cryostat limited us to temperatures
above
and 0.6 Tc.
The field dependence at lower T was not investigated because
the 4He gas flow cryostat limited us to temperatures
above ![]() K.
In the Meissner state of a conventional s-wave superconductor,
K.
In the Meissner state of a conventional s-wave superconductor,
![]() is expected to increase
quadratically as a function of magnetic field, due to nonlinear effects.
The nonlinear corrections to the supercurrent response
are the same in both the Meissner and vortex states.
However, the average supercurrent density
is expected to increase
quadratically as a function of magnetic field, due to nonlinear effects.
The nonlinear corrections to the supercurrent response
are the same in both the Meissner and vortex states.
However, the average supercurrent density
![]() scales quite differently in the
Meissner and vortex states, as shown in Fig. 6.7. The
curve in the top panel of Fig. 6.7 (i.e. the Meissner state)
was generated
assuming that the magnetic field decays exponentially
[see Eq. (2.15)] and that
scales quite differently in the
Meissner and vortex states, as shown in Fig. 6.7. The
curve in the top panel of Fig. 6.7 (i.e. the Meissner state)
was generated
assuming that the magnetic field decays exponentially
[see Eq. (2.15)] and that ![]() is field independent.
Thus in the Meissner state,
is field independent.
Thus in the Meissner state, ![]() .It follows that if
.It follows that if ![]() , then
, then
![]() .
.
The solid curve in the bottom panel of Fig. 6.7
(i.e. the vortex state)
was generated with the field profile ![]() from the analytical
GL model. The dashed curve in this figure shows that the average
supercurrent density in the vortex state is approximately proportional to
from the analytical
GL model. The dashed curve in this figure shows that the average
supercurrent density in the vortex state is approximately proportional to
![]() . Thus, if
. Thus, if
![]() and
and
![]() (as measured here), then as in the Meissner
state
(as measured here), then as in the Meissner
state ![]() .This suggests that the field dependence of
.This suggests that the field dependence of ![]() in the
vortex state of NbSe2 is due to nonlinear effects.
However,
in the
vortex state of NbSe2 is due to nonlinear effects.
However, ![]() measured in our
measured in our ![]() SR experiment is by definition
not the same as the penetration depth which appears in the nonlinear theory
or which is measured in the Meissner state.
Relating
SR experiment is by definition
not the same as the penetration depth which appears in the nonlinear theory
or which is measured in the Meissner state.
Relating ![]() from the
nonlinear theory to the effective
from the
nonlinear theory to the effective
![]() measured by
measured by ![]() SR is nontrivial and
requires a proper account of the vortex source term.
SR is nontrivial and
requires a proper account of the vortex source term.
In the vortex state, the strength of the term which is linear in H is
almost the same at both temperatures considered, when normalized with
respect to
the value of Hc2 (T) (see parameter
![]() in Table 6.3).
As the temperature is increased, the energy gap in the quasiparticle
excitation spectrum shrinks, leading to the thermal
excitation of quasiparticles.
The reduction in the size of the energy gap also means that quasiparticles
can be excited by relatively smaller magnetic fields.
For this reason, in the Meissner state, the strength of the term
quadratic in H
is found to increase with increasing T.
Since the strength of the coefficient
in Table 6.3).
As the temperature is increased, the energy gap in the quasiparticle
excitation spectrum shrinks, leading to the thermal
excitation of quasiparticles.
The reduction in the size of the energy gap also means that quasiparticles
can be excited by relatively smaller magnetic fields.
For this reason, in the Meissner state, the strength of the term
quadratic in H
is found to increase with increasing T.
Since the strength of the coefficient ![]() for the term linear in H in
Eq. (6.1)
does not appear to change over a large range of temperature
in the vortex state, it seems unlikely that the mechanism responsible
for the nonlinear Meissner effect can be solely responsible for the
observed
H-dependence of
for the term linear in H in
Eq. (6.1)
does not appear to change over a large range of temperature
in the vortex state, it seems unlikely that the mechanism responsible
for the nonlinear Meissner effect can be solely responsible for the
observed
H-dependence of ![]() in the vortex state.
Furthermore, according to the calculations of Amin et al. [40],
it seems unlikely that nonlinear corrections to the supercurrent response
in the vortex state can result in a field dependence for the effective
penetration depth measured by
in the vortex state.
Furthermore, according to the calculations of Amin et al. [40],
it seems unlikely that nonlinear corrections to the supercurrent response
in the vortex state can result in a field dependence for the effective
penetration depth measured by ![]() SR which is as strong
as that found here. However, as just mentioned, the calculation of the
effective
SR which is as strong
as that found here. However, as just mentioned, the calculation of the
effective ![]() is rather sensitive to the vortex source term,
so that the size of the vortex cores should be included in such calculations.
is rather sensitive to the vortex source term,
so that the size of the vortex cores should be included in such calculations.
| Equation | 2c| |
2c| |
||
| [Å] | [Å] | |||
| 1323(2) | 1.62(3) | 1436(3) | 1.56(2) | |
| 8.4 (2) | 7.4 (2) | 5.7(2) | 8.2(3) | |
| 6.9(2) | 9.5(3) | 5.1(2) | 10.2(4) | |
Since ![]() is not the only parameter which contributes
to the fitted
is not the only parameter which contributes
to the fitted ![]() SR line width, it is necessary to monitor the behaviour
of the additional broadening parameter
SR line width, it is necessary to monitor the behaviour
of the additional broadening parameter ![]() . Besides
disorder in the vortex lattice, the large 93Nb nuclear moments
(
. Besides
disorder in the vortex lattice, the large 93Nb nuclear moments
(![]() ) in NbSe2
also slightly broaden the
) in NbSe2
also slightly broaden the ![]() SR line shape.
For instance, in the normal state the muon depolarization rate
SR line shape.
For instance, in the normal state the muon depolarization rate ![]() at
at ![]() K is found to increase linearly
from
K is found to increase linearly
from ![]() at
at ![]() T to
T to ![]() at
at
![]() T. To determine the degree of disorder
in the vortex lattice, the contribution of the 93Nb
nuclear moments
T. To determine the degree of disorder
in the vortex lattice, the contribution of the 93Nb
nuclear moments ![]() to the muon depolarization rate
can be subtracted in quadrature from the fitted value of
to the muon depolarization rate
can be subtracted in quadrature from the fitted value of ![]()
| (2) |
![\begin{displaymath}
\langle s^2 \rangle^{\frac{1}{2}} \approx \frac{\sigma_{\rm ...
...^2 \lambda_{ab}^2/(1-b) \right]^2}
\right)^{- \frac{1}{2}} \, .\end{displaymath}](img473.gif) |
(3) |
For a perfect triangular vortex lattice the intervortex spacing is given by
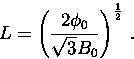 |
(4) |
The radius of a vortex core is not a uniquely defined quantity, since
there exists no sharp discontinuity between a normal vortex core and the
superconducting material. Nevertheless, a useful definition can be made
taking into account the dramatic spatial changes observed in quantities
such as the order parameter ![]() , the local density of
states
, the local density of
states ![]() ,
the supercurrent
density
,
the supercurrent
density ![]() and the local magnetic field strength
and the local magnetic field strength ![]() near the center of a vortex line.
Since the supercurrent density
near the center of a vortex line.
Since the supercurrent density ![]() can be easily obtained
from the fitted field profile through the Maxwell relation
can be easily obtained
from the fitted field profile through the Maxwell relation
![]() , we define an effective core radius r0 to be
the distance from the vortex center for which Js (r) reaches
its maximum value. As shown in Fig. 6.10, Js (r) rises steeply
from zero at the vortex center to its maximum
value
, we define an effective core radius r0 to be
the distance from the vortex center for which Js (r) reaches
its maximum value. As shown in Fig. 6.10, Js (r) rises steeply
from zero at the vortex center to its maximum
value ![]() at r0.
at r0.
The magnetic field dependence of r0 in NbSe2 is shown in
Fig. 6.11, where r0 is obtained from Js (r) profiles
created from the fitted field profiles B (r). The deduced
values of r0 are less sensitive (than ![]() ) to the choice
of the theoretical model for B (r). This is because a good
approximation of Js (r) can be obtained by taking the
curl of any function B (r) which fits the measured
field distribution well.
This includes an insensitivity to the assumed
vortex-lattice geometry, provided a good fit is obtained.
Since r0 is fairly robust to the validity of the theoretical field
distribution used to fit the data, then provided a good fit is obtained,
the vortex-core
radius can be determined from
) to the choice
of the theoretical model for B (r). This is because a good
approximation of Js (r) can be obtained by taking the
curl of any function B (r) which fits the measured
field distribution well.
This includes an insensitivity to the assumed
vortex-lattice geometry, provided a good fit is obtained.
Since r0 is fairly robust to the validity of the theoretical field
distribution used to fit the data, then provided a good fit is obtained,
the vortex-core
radius can be determined from ![]() SR with few
theoretical assumptions. We note that discrepancies
between the three
models considered here do appear at low fields (see Fig. 6.11)
because of the reduced statistics at the high-field tail
of the measured internal field distribution. Since there are far
fewer vortices in the sample at these low fields,
there is a reduction
in the number of events originating from muons which
stop in the vicinity of the vortex cores. As a result, the
high-field tail shows more ``statistical wiggles'', which in turn
allows for a greater variation in the tail of the fitted B (r).
Increasing
the number of recorded muon decay events in the
SR with few
theoretical assumptions. We note that discrepancies
between the three
models considered here do appear at low fields (see Fig. 6.11)
because of the reduced statistics at the high-field tail
of the measured internal field distribution. Since there are far
fewer vortices in the sample at these low fields,
there is a reduction
in the number of events originating from muons which
stop in the vicinity of the vortex cores. As a result, the
high-field tail shows more ``statistical wiggles'', which in turn
allows for a greater variation in the tail of the fitted B (r).
Increasing
the number of recorded muon decay events in the ![]() SR spectra
at low H would rectify this problem and should lead to better agreement
between the three models in Fig. 6.11 at all magnetic fields.
SR spectra
at low H would rectify this problem and should lead to better agreement
between the three models in Fig. 6.11 at all magnetic fields.
Golubov and Hartmann [205] have shown that the shrinking
of the vortex core radius with increasing magnetic field can be
attributed to increased vortex-vortex interactions. They solved
the microscopic equations in the dirty limit (i.e. the Usadel
equations) self-consistently and showed that the order parameter
![]() and the LDOS reach their maximum
values closer to the vortex
center when H is increased. From the LDOS, these authors calculated
tunneling current I(r) profiles from the vortex center as a
function of H in order to model STM measurements of r0 (H) in
NbSe2 [206]. The magnetic field dependence of
r0 in NbSe2 determined by STM at
and the LDOS reach their maximum
values closer to the vortex
center when H is increased. From the LDOS, these authors calculated
tunneling current I(r) profiles from the vortex center as a
function of H in order to model STM measurements of r0 (H) in
NbSe2 [206]. The magnetic field dependence of
r0 in NbSe2 determined by STM at ![]() is shown in Fig. 6.12 along with that determined
by
is shown in Fig. 6.12 along with that determined
by ![]() SR at
SR at ![]() and 0.33 Tc.
The definition of r0 in the STM experiment was
arbitarily chosen to be the radius at which the measured I(r) had diminished
to
and 0.33 Tc.
The definition of r0 in the STM experiment was
arbitarily chosen to be the radius at which the measured I(r) had diminished
to ![]() of its maximum value at the vortex-core center.
It was shown in Ref. [205] that this gives a value of r0
which is somewhat larger than the commonly used theoretical
definition, i.e. the radius at which
of its maximum value at the vortex-core center.
It was shown in Ref. [205] that this gives a value of r0
which is somewhat larger than the commonly used theoretical
definition, i.e. the radius at which
![]() rises from zero at the core center to
rises from zero at the core center to ![]() of its maximum
value well away from the core.
The different definitions of r0 are the main reason for the
difference in magnitude of r0 between the STM and
of its maximum
value well away from the core.
The different definitions of r0 are the main reason for the
difference in magnitude of r0 between the STM and ![]() SR experiments
at
SR experiments
at ![]() .
Also, we found from the microscopic theory (see Ref. [4])
that Js (r)
does not reach its maximum value at exactly the radius
where
.
Also, we found from the microscopic theory (see Ref. [4])
that Js (r)
does not reach its maximum value at exactly the radius
where ![]() reaches
reaches ![]() of its maximum value, at
all temperatures and magnetic fields. For this reason, our definition
of r0 is robust to changes in T and H and should
better reflect the actual H-dependence of the vortex-core
radius.
of its maximum value, at
all temperatures and magnetic fields. For this reason, our definition
of r0 is robust to changes in T and H and should
better reflect the actual H-dependence of the vortex-core
radius.
The authors of Ref. [205] reported good agreement between
the STM measurements of r0 (H) and the dirty-limit microscopic
theory. Although the magnitude of r0 is reasonably predicted from
their calculations, the error bars in the STM measurements are too
large to conclude whether there is precise agreement with the theory.
In a ![]() SR experiment, typically
SR experiment, typically ![]() muons sample
the local magnetic field of
approximately 1011 vortices in the bulk of a few mm2 sample,
as opposed to an STM experiment which averages r0 from a few
vortices at the surface. As a result of this statistical improvement,
the
muons sample
the local magnetic field of
approximately 1011 vortices in the bulk of a few mm2 sample,
as opposed to an STM experiment which averages r0 from a few
vortices at the surface. As a result of this statistical improvement,
the ![]() SR data shown in Fig. 6.12
have smaller error bars and less scatter.
This improvement allowed us to show in Ref. [4] that
r0 decreases more strongly with magnetic field than predicted
by the dirty-limit microscopic theory. This finding was not surprising
since NbSe2 is in the clean limit. To our knowledge, there have
yet to be any calculations of the H-dependence of r0 from the
microscopic theory in the clean limit. However, in Ref. [4]
we showed that the
SR data shown in Fig. 6.12
have smaller error bars and less scatter.
This improvement allowed us to show in Ref. [4] that
r0 decreases more strongly with magnetic field than predicted
by the dirty-limit microscopic theory. This finding was not surprising
since NbSe2 is in the clean limit. To our knowledge, there have
yet to be any calculations of the H-dependence of r0 from the
microscopic theory in the clean limit. However, in Ref. [4]
we showed that the ![]() SR results fit well to the simple phenomenological
equation
SR results fit well to the simple phenomenological
equation
![\begin{displaymath}
r_0(H) = \frac{\lambda_{ab} (H)}{\kappa^\prime (H)} = r_0(0)...
...c{\left[ 1 + \beta h \right]}{\left[ 1 + \gamma h \right]} \, ,\end{displaymath}](img489.gif) |
(5) |
The effective coherence length ![]() in
Eq. (4.13) which best fits the data is
plotted in Fig. 6.13 as a function of magnetic field.
The variation of
in
Eq. (4.13) which best fits the data is
plotted in Fig. 6.13 as a function of magnetic field.
The variation of ![]() is similar to that of r0(H,T), which
was shown earlier to be model independent.
The curves through the data points were generated from the fitted
relations for
is similar to that of r0(H,T), which
was shown earlier to be model independent.
The curves through the data points were generated from the fitted
relations for ![]() and
and ![]() given in Table 6.3.
It should be kept in mind
that
given in Table 6.3.
It should be kept in mind
that ![]() must be considered an ``effective'' coherence
length. For instance, according to Eq. (2.73) of the GL theory,
the coherence length near Hc2 at
must be considered an ``effective'' coherence
length. For instance, according to Eq. (2.73) of the GL theory,
the coherence length near Hc2 at ![]() should be
106.5 Å, where
should be
106.5 Å, where ![]() T.
However, at 2.9 T the fitted curve in Fig. 6.13 gives
T.
However, at 2.9 T the fitted curve in Fig. 6.13 gives
![]() Å. Similarly, at
Å. Similarly, at
![]() , Eq. (2.73)
yields
, Eq. (2.73)
yields ![]() Å, whereas the fitted curve in
Fig. 6.13 gives 78.7 Å.
A reduced value of
Å, whereas the fitted curve in
Fig. 6.13 gives 78.7 Å.
A reduced value of ![]() may be obtained
if the fitted theoretical field distribution overestimates the length
of the high-field tail in the
may be obtained
if the fitted theoretical field distribution overestimates the length
of the high-field tail in the ![]() SR line shape. However,
according to Fig. 6.5, it is highly
unlikely that the fits are substantially overestimating the length of
the high-field tail. The discrepancy between
the measured
SR line shape. However,
according to Fig. 6.5, it is highly
unlikely that the fits are substantially overestimating the length of
the high-field tail. The discrepancy between
the measured ![]() and that predicted in Eq. (2.73)
is most likely due to the theoretical difference between
and that predicted in Eq. (2.73)
is most likely due to the theoretical difference between
![]() in Eq. (4.13) and the ``true'' GL coherence length.
Given that GL theory is really only valid near the phase boundary,
it is reasonable that deviations occur at low T and low H.
in Eq. (4.13) and the ``true'' GL coherence length.
Given that GL theory is really only valid near the phase boundary,
it is reasonable that deviations occur at low T and low H.
Assuming that the shrinking of the cores is associated with the strength of
the vortex-vortex interactions,
the increase in r0 and ![]() with decreasing magnetic field
should saturate when the vortices are sufficiently far apart (i.e. when
with decreasing magnetic field
should saturate when the vortices are sufficiently far apart (i.e. when
![]() ). From Eq. (6.4) and the fitted
expressions for
). From Eq. (6.4) and the fitted
expressions for ![]() in Table 6.3, the field at
which this saturation occurs can be estimated. In particular,
at
in Table 6.3, the field at
which this saturation occurs can be estimated. In particular,
at ![]() there should be no change in the size of the
vortex cores below
there should be no change in the size of the
vortex cores below ![]() T, whereas this crossover field
is
T, whereas this crossover field
is ![]() T at
T at ![]() .
.
A few remarks are now necessary with regard to
the behaviour of ![]() and
and
![]() in Fig. 6.14.
The behaviour of
in Fig. 6.14.
The behaviour of ![]() implies that NbSe2 becomes more type-II like
with increasing magnetic field.
In GL theory,
implies that NbSe2 becomes more type-II like
with increasing magnetic field.
In GL theory, ![]() is independent
of both H and T. However, this definition
is strictly valid only near the superconducting-to-normal phase
transition. Our results imply that the conventional GL equations
with field-independent
is independent
of both H and T. However, this definition
is strictly valid only near the superconducting-to-normal phase
transition. Our results imply that the conventional GL equations
with field-independent ![]() and
and ![]() are not applicable
deep in the superconducting state.
Even if
are not applicable
deep in the superconducting state.
Even if ![]() were field independent, an
increase of
were field independent, an
increase of ![]() and
and ![]() with H would still
arise from the decrease of
with H would still
arise from the decrease of ![]() which has been independently
observed in NbSe2 by STM. Furthermore, attempts to fix
which has been independently
observed in NbSe2 by STM. Furthermore, attempts to fix
![]() and
and ![]() to constant values
in the fitting procedure yield higher values of
to constant values
in the fitting procedure yield higher values of
![]() and unphysical results--such as a
residual background signal which is
and unphysical results--such as a
residual background signal which is ![]() of the total signal
amplitude.
of the total signal
amplitude.
Figure 6.15 shows a typical muon precession signal
displayed for convenience in a reference frame rotating at
about 1.5 MHz below the Larmor precession frequency of a free muon.
The curves through the data points are examples of fits to
the theoretical polarization function for fixed values of ![]() , where
, where
![]() and all other parameters were free to vary.
Only the first 3
and all other parameters were free to vary.
Only the first 3 ![]() s of data are shown in Fig. 6.15 since
the signal from the vortex lattice essentially decays over this
time range--although the fits were actually performed over the first 6
s of data are shown in Fig. 6.15 since
the signal from the vortex lattice essentially decays over this
time range--although the fits were actually performed over the first 6 ![]() s.
Figure 6.16 shows the difference between the data points
and the fitted curve for the fits in
Fig. 6.15. There is a clear oscillation for the
fits corresponding to
s.
Figure 6.16 shows the difference between the data points
and the fitted curve for the fits in
Fig. 6.15. There is a clear oscillation for the
fits corresponding to ![]() Å and
Å and
![]() Å, indicating a missed frequency or frequencies.
The ratio of
Å, indicating a missed frequency or frequencies.
The ratio of ![]() to the number of degrees of freedom (NDF)
is shown in Fig. 6.17(a) as a function of
to the number of degrees of freedom (NDF)
is shown in Fig. 6.17(a) as a function of ![]() for two
different applied magnetic fields. Note that the value of
for two
different applied magnetic fields. Note that the value of ![]() for which
for which ![]() /NDF reaches its minimum value is quite different
for the two fields. Figure 6.17(b) shows the behaviour of
the free parameter
/NDF reaches its minimum value is quite different
for the two fields. Figure 6.17(b) shows the behaviour of
the free parameter ![]() for these same fits.
The best fits indicate that
for these same fits.
The best fits indicate that ![]() is dependent on magnetic field.
is dependent on magnetic field.
The reduction in r0 and ![]() with increasing temperature
which is shown in Fig. 6.12 and Fig. 6.13, respectively,
is expected from theoretical predictions for a s-wave vortex
[140,148,150]. However, as shown in
Fig. 6.18(b), the
vortex core radius does not decrease as steeply with temperature as
predicted by theory. The dashed line in
Fig. 6.18(b) is a fit
to the theory of Kramer and Pesch [140]
[see Eq. (4.11)] where
with increasing temperature
which is shown in Fig. 6.12 and Fig. 6.13, respectively,
is expected from theoretical predictions for a s-wave vortex
[140,148,150]. However, as shown in
Fig. 6.18(b), the
vortex core radius does not decrease as steeply with temperature as
predicted by theory. The dashed line in
Fig. 6.18(b) is a fit
to the theory of Kramer and Pesch [140]
[see Eq. (4.11)] where ![]() ,with
,with ![]() Å.
Part of the problem is that these theoretical
calculations pertain to a single isolated vortex.
Given the apparent strong influence of vortex-vortex interactions,
the vortex-lattice
effect should not be ignored in theoretical calculations for r0 (T).
For a given magnetic field,
Å.
Part of the problem is that these theoretical
calculations pertain to a single isolated vortex.
Given the apparent strong influence of vortex-vortex interactions,
the vortex-lattice
effect should not be ignored in theoretical calculations for r0 (T).
For a given magnetic field, ![]() will grow with
increasing temperature [see Fig. 6.18(a)],
whereas the intervortex spacing L remains constant. The strength
of the vortex-vortex interactions will increase at higher field as the ratio
will grow with
increasing temperature [see Fig. 6.18(a)],
whereas the intervortex spacing L remains constant. The strength
of the vortex-vortex interactions will increase at higher field as the ratio
![]() increases, leading to additional changes in the electronic
structure of the vortex cores. Since these interactions become stronger
with increasing T, the difference between the measured value of r0
and that predicted for an isolated vortex core will increase
monotonically with temperature.
increases, leading to additional changes in the electronic
structure of the vortex cores. Since these interactions become stronger
with increasing T, the difference between the measured value of r0
and that predicted for an isolated vortex core will increase
monotonically with temperature.
The solid line through the data in Fig. 6.18(a) is a fit to
the empirical relation ![]() with
with ![]() m-2,
m-2,
![]() and
and ![]() .Although this is considered to be consistent with a
weak-coupling BCS superconductor [1]
(which shows a T-dependence of
.Although this is considered to be consistent with a
weak-coupling BCS superconductor [1]
(which shows a T-dependence of ![]() which is close
to (1-t2)), there is no real low temperature data to obtain
a proper fit to the BCS expression of Eq. (2.27).
From the empirical fit and an observed weak
linear-T dependence for
which is close
to (1-t2)), there is no real low temperature data to obtain
a proper fit to the BCS expression of Eq. (2.27).
From the empirical fit and an observed weak
linear-T dependence for ![]() ,the temperature dependence of the vortex-core radius is given by
,the temperature dependence of the vortex-core radius is given by
![\begin{displaymath}
r_0(T) = \frac{\lambda_{ab} (T)}{\kappa^\prime (T)} = r_0(0)...
...^p \right]^{-\frac{1}{2}} \left[ 1 - \gamma t \right]^{-1} \, ,\end{displaymath}](img519.gif) |
(6) |